Automatic Movie Content Analysis
The MoCA Project 
The MoCA Project
MoCA Project: Video Color Adaptation for Mobile Devices
A large number of videos cannot be visualized on mobile devices
(e.g., PDAs or mobile phones) due to an inappropriate color depth of
the displays. Important details are lost if the color depth is
reduced. A major challenge is the preservation of the semantic content
in spite of this fact. We present a novel adaptation algorithm to
enable the playback of videos on color-limited mobile devices.
Dithering algorithms diffuse the error to neighbor pixels and do not
work very well for videos. We propose a non-linear transformation of
luminance values and use textures in combination with edges to reduce
the the color depth in videos.
Videos are no longer limited to television or personal computers
due to the technological progress in the last years. Nowadays, many
different devices such as Tablet-PCs, Handheld-PCs, PDAs, notebooks or
mobile phones support the playback of videos. The specific
features of a particular mobile device (e.g., the color depth of the
display or the performance of the CPU) must be considered to achieve a
reasonable playback quality of videos. We focus on the color
depth as one of the main features affecting the quality of videos.
Automatic video adaptation techniques facilitate the playback of
videos especially for mobile devices. For such techniques, the
most important goal is the preservation of the semantic information in
the adapted video. Although much work was done on the transcoding
of videos only few approaches focus on the semantic adaptation [1, 3, 4].
Adaptation of the Color Depth
By reducing the color depth of an image large regions with
identical colors appear, and it becomes much more difficult to
recognize details in the images. Especially, the adaptation of videos
for monochrome displays - where all pixels are represented with two
different luminance values - is not easily archivable.
The conversion from color to grayscale is done without any
computational effort because most video compression standards store
luminance and color values separately. The number of different
luminance values can be reduced by defining equal-sized intervals and
linearly mapping all luminance values in each interval to a new value.
A variable interval size
derived from the distribution of the luminance values in the source
image improves the quality of the adapted image significantly. We
use cumulated histograms Hkum (i) to define the non-linear
transformation of the luminance values:
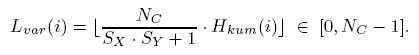
The width Sx and height Sy of the image normalize the cumulated
histogram. The transformation of the luminance i to the new value Lvar
(i) depends on the distribution of the histogram values and the number
of different colors Nc in the adapted image. Figure 1 (b) exemplifies
adapted images with Nc=8 different luminance values by applying a
linear transformation with equal-sized intervals (equal-sized bins).
Fine structures and details are lost. Much more details are discernible
if a variable interval size is applied compared to the linear
transformation (see Figure 1 (c)).

An extension for the adaptation of videos is considered i the
following. Significant luminance changes are visible if we analyze the
cumulated histograms for each frame. Therefore, we calculate one
aggregated cumulated histogram for all frames of a shot. The histogram
describes the distribution of the luminance values of this shot.
Suitable parameters Lvar(i) can be derived from the
cumulated histogram. The adaptation for binary displays is considered
in a second step. The problem to represent a color image with few
different colors is well known from printing. One method is called
Halftoning: Different colors are combined to create the illusion of a
new color.
In 1975, the well-known Floyd/Steinberg dithering algorithm was
published that reduces the perceptible error when the color depth of an
image is reduced [2]. The algorithm maps each pixel to a new value and
diffuses the error to neighbor pixels. In spite of the good results for
images, this algorithm cannot be applied for video sequences because
many pixels change between adjacent frames due to the diffusion of
errors. Hence, the content in such videos is no longer recognizable.
In the following, we describe the details of our algorithm which
uses binary textures to
substitute the pixels of an image. A grayscale image with Nc=16
different luminance values is constructed with cumulated histograms,
and each value is substituted with pixels from the corresponding
texture. In some cases, the differences between two adjacent regions
are quite low. This leads to good results for gradual transitions
(e.g., the sky in Figure 2 (a)) but strong edges in the image are lost.
We compensate the loss of details by overlaying the textured image with
an edge image. This approach emphasizes significant edge pixels (e.g.,
the roof in Figure 2 (b)).
(click on the image to see a large version)
We presented an algorithm to reduce the color depth of images while
original semantics are preserved. Furthermore, our novel algorithm
transcodes videos so that they can be displayed on monochrome displays.
We have shown the performance of our approach by examples. A video demo
is available at the end of this web page.
References
| [1] |
L.-Q. Chen, X. Xie, X. Fan, W.-Y. Ma, H.-J. Zhang, and H.-Q. Zhou. A visual attention model for adapting images on small displays. In ACM Multimedia Systems Journal, volume 9(4), pages 353 - 364. ACM Press, 2003. |
| [2] |
R. Floyd and L. Steinberg. An adaptive algorithm for spatial grey scale. In Journal of the Society for Information Display, volume 17(2), pages 75 - 77, 1976. |
| [3] |
J.-G. Kim, Y. Wang, and S.-F. Chang. Content-adaptive utility-based video adaptation. In Proceedings of IEEE International Conference on Multimedia and Expo (ICME), pages 281 - 284. IEEE Computer Society Press, July 2003 |
| [4] |
R. Mohan, J. Smith, and C. Li. Adapting multimedia internet content for universal access. In IEEE Transactions on Multimedia, volume 1(1), pages 104 - 114. IEEE Computer Society Press, March 1999. |
Video Demo
| Demo of the color adaptation algorithm |
 |
MPEG-2 Video (360 MB) Windows Media Video (56 MB) |
Video Example
| Color adaptation results |
 |
MPEG-2 Video (65 MB) Windows Media Video (17 MB) |

