
So verwendet man z.B. bei bestimmten Datenbankkonzepten Hashfunktionen, um zu entscheiden, an welcher Stelle man einen Datensatz in die Datenbank einfügt. Man bildet den Hashwert der Schlüsselfelder - Wertebereich ist hier stets die Anzahl der zur Verfügung stehenden Datenblöcke - und fügt den Datensatz im so ermittelten Block ein. ist der Block bereits belegt, liegt eine "Kollision" vor, und ein neuer Block muß gefunden werden. Da mit steigender Anzahl der Kollisionen die Effizienz des Einfügens und Suchens in der Datenbank nachläßt, ist man hier besonders an einer gleichmäßigen Verteilung interessiert.
Hashfunktionen können auch als Prüfsummen eingesetzt werden, und da kommen wir dem Einsatzzweck "Signaturen" schon näher. Eine Prüfsumme hat zwei wichtige Kriterien zu erfüllen:
Die zweite Forderung erscheint zunächst schwächer, als sie es tatsächlich ist. Die Stärke der modernen Kryptoverfahren liegt ja gerade darin, daß außer den Schlüsseln der Beteiligten nichts "Geheimes" an ihnen ist, nichts, was entdeckt und veröffentlich werden könnte und das ganze System lahmlegt.
Aus der zweiten Forderung ergibt sich auch die Notwendigkeit, daß eine kleine Änderung im Urbild eine große (d.h. nicht direkt nachvollziehbare) Änderung im Funktionswert nach sich ziehen sollte. Wäre das nicht der Fall und könnte man beispielsweise einzelne Bits des Funktionswertes direkt durch Änderungen am Urbild beeinflussen (wie das bei der XOR-Funktion der Fall ist), so wäre es ein leichtes, zu einem gegebenen Funktionswert ein geeignetes Urbild zu erstellen.

| ohne Hashfunktion | mit Hashfunktion
| Alice will Bob ein signiertes Dokument
"D" senden. | Alice will Bob ein signiertes Dokument
"D" senden.
| | Alice bildet den Hashwert H(D).
| Alice verschlüsselt D mit ihrem privaten
Schlüssel und erhält das verschlüsselte
Dokument E(D), das sie an Bob sendet. | Alice
verschlüsselt H(D) mit ihrem privaten
Schlüssel und erhält E(H(D)).
Alice sendet D und E(H(D)) an Bob.
| Bob entschlüsselt E(D) mit Alices
öffentlichem Schlüssel. | Bob
entschlüsselt E(H(D)) mit Alices öffentlichem
Schlüssel.
| Bob bildet mit der ihm ebenfalls bekannten
Hashfunktion H selbst H(D) und vergleicht den Wert mit
dem H(D), das er entschlüsselt hat.
| | Bob hat nun H(D) und weiß: "Alice
hat ein Dokument X mit H(X) = H(D) unterschrieben".
| Bob weiß nun: "Alice hat D
unterschrieben.". | Da die Funktion H eine "one-way"-
Funktion ist, ist davon auszugehen, daß X=D, also
hat Alice D unterschrieben.
| |
|---|
Hier wird klar: Wenn es auch nur die geringste Chance für Bob gäbe, ein anderes Dokument A zu erzeugen, für das H(A)=H(D) gilt, so könnte er behaupten, er habe A zusammen mit Alices Signatur erhalten und nicht D, denn Alice hat nicht das Dokument, sondern nur den Hashwert unterschrieben. Deshalb ist die Forderung nach der one-way-Eigenschaft so entscheidend.
Viel einfacher ist es jedoch, zwei Dokumente herzustellen, die denselben Hashwert besitzen (eine "Kollision"). Die damit möglichen Betrügereien sind etwas subtiler; man müßte dann versuchen, eine Person unter Vorspiegelung falscher Tatsachen zu einer Unterschrift unter A zu bewegen, um dann auch eine gültige Unterschrift für B zu haben.
Diese zweite Attacke wird auch "Birthday Attack" genannt. Dem liegt das sogenannte "Geburtstagsparadoxon" zugrunde: In einem Raum müßten 183 Personen sein, damit mit einer Wahrscheinlichkeit größer 50 % eine Person anwesend ist, die den gleichen Geburtstag hat wie der Gastgeber. Es müssen aber nur 23 sein, um mit einer Wahrscheinlichkeit größer 50 % zwei Personen mit demselben (aber beliebigen) Geburtstag zu finden.
Dies ist statistisch unmittelbar einleuchtend (und hat daher den Namen "Paradoxon" vielleicht nicht ganz verdient), für viele aber dennoch ein verblüffendes Ergebnis.
Angenommen, man arbeitet mit 64-Bit-Hashwerten, so würde es (bei einer Rechenleistung von 1 Mio. Hashwerten pro Sekunde) rund 600.000 Jahre dauern, bis ein zweites Dokument mit dem gleichen Hashwert wie ein vorgegebenes Dokument gefunden wäre. Um ein Paar von Dokumenten mit übereinstimmendem Hashwert zu finden, benötigte derselbe Rechner aber nur rund eine Stunde.
Um die Hashfunktion sicher gegenüber der Geburtstagsattacke zu machen, sollte man mit 160-Bit- Hashwerten arbeiten.
Zahlreiche Versuche sind unternommen worden, "sichere" one-way-Hashfunktionen zu erzeugen; viele der Ergebnisse sind inzwischen (nachdem sie lange eingesetzt wurden) als unzureichend sicher eingestuft worden, und auch die MD5-Hashfunktion, die wir hier exemplarisch vorstellen werden, ist nicht "erwiesenermaßen sicher".
MD5 arbeitet in 4 Runden und mit 64 Konstanten. Das Ergebnis ist ein 128-Bit-Hashwert. Sein Ablauf läßt sich in vier Schritten darstellen:
Schritt 1: Padding der Nachricht
In einem ersten Schritt muß die Nachricht auf ein
Vielfaches von 512 Bit ergänzt werden, da die
Hauptiterationsfunktion mit 512-Bit-Blöcken
arbeitet. Dazu wird sie auf eine Länge kongruent
448 modulo 512 gebracht, indem an die Nachricht zuerst
eine einzelne 1 angehängt wird und dann noch
soviele Nullen, bis die Nachricht kongruent 448 modulo
512 ist. (Das Anhängen der 1 stellt sicher,
daß die Nachricht mindestens eine Eins
enthält.) Der schlimmste Fall ist eine 448 Bit
lange Nachricht; sie wird hierbei durch das Padden auf
960 Bit erweitert, da sie nach Anhängen der Eins
eine Länge von 449 Bit besitzt, weshalb sie dann
mit 511 Nullen ergänzt wird.
In die letzten 64 freien Bit wird die Länge der ursprünglichen Nachricht geschrieben; daher kann MD5 nur Nachrichten von einer Länge kleiner 264 verarbeiten.
Schritt 2: Initialisierung
Bei der Berechnung werden vier 32-Bit-Puffer verwendet,
die den aktuellen Rundenhashwert mit einer
Größe von 128 Bit beinhalten. Diese
müssen, da MD5 eine iterative Hashfunktion ist,
initialisiert werden; dafür werden die folgenden
Werte benutzt:
h(0) := 76543210hex
h(1) := fedcba98hex
h(2) := 98abcdefhex
h(3) := fedcba89hex
(Die Zahlen sind in der low-byte-first-Notation
angegeben.)
Schritt 3: Berechnung des
Blockhashwertes
In diesem Schritt werden 64 Funktionen ft(x,y,z), 64
Konstanten K(t), 64 Rotationskonstanten Rtund die
16 Worte W(i) des aktuellen Blockes in
Abhängigkeit der jeweiligen Prozeßstufe
verwendet. Die Funktionen ft sind folgendermaßen
definiert:
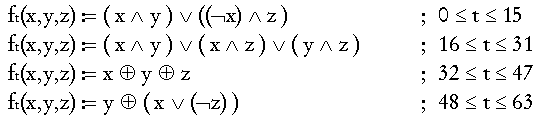
Die 64 verwendeten additiven Konstanten Kt leiten sich
aus irrationalen Zahlen, in Abhängigkeit der
zugehörigen Prozeßstufe, wie folgt ab:

Die Rotationskonstanten sind in folgender Tabelle
angegeben:
| Rt | t div 16 | |||
| t mod 4 | 0 | 1 | 2 | 3 |
| 0 | 7 | 5 | 4 | 6 |
| 1 | 12 | 9 | 11 | 10 |
| 2 | 17 | 14 | 16 | 15 |
| 3 | 22 | 20 | 23 | 21 |
Da jede Konstante viermal benutzt wird, sind es in Wirklichkeit nur 16 Rotationskonstanten. Die Berechnung des Hashwertes nach MD5 sieht algorithmisch nun so aus:
A := h0 B := h1 C := h2 D := h3 FOR t = 0 TO 63 DO BEGIN T := B + ((A + ft(B,C,D) + W(t) + Kt), Rk) B := A A := D D := C C := T END h0 := h0 + A h1 := h1 + B h2 := h2 + C h3 := h3 + D
| Hash-Algorithmus | Länge des Hashwertes | Geschwindig-keit (MB/Sek.) |
|---|---|---|
| Abreast Davies-Meyer (mit IDEA) | 128 | 22 |
| Davies-Meyer (mit DES) | 64 | 9 |
| GOST Hash | 256 | 11 |
| Haval (3 Durchgänge) | variabel | 168 |
| Havel (4 Durchgänge) | variabel | 118 |
| Haval (5 Durchgänge) | variabel | 95 |
| MD2 | 128 | 23 |
| MD4 | 128 | 236 |
| MD5 | 128 | 174 |
| N-Hash (12 Runden) | 128 | 29 |
| N-Hash (15 Runden) | 128 | 24 |
| Ripe-MD | 128 | 182 |
| SHA | 160 | 75 |
| SNEERU (4 Durchgänge) | 128 | 48 |
| SNEERU (8 Durchgänge) | 128 | 23 |
Beispielsweise ist es einem Erfinder möglich, zur Sicherung seiner Rechte einen Hashwert seiner Unterlagen zu bilden und diesen zu veröffentlichen. Zu jedem späteren Zeitpunkt kann er nachweisen, daß er diese Unterlagen schon zum Zeitpunkt der Veröffentlichung besessen hat, indem er sie vorlegt und jeder prüfen kann, daß sich daraus tatsächlich der vor Jahren veröffentlichte Hash-Wert ergibt. Hätte der Erfinder inzwischen die kleinste Änderung an den Dokumenten vorgenommen, würde der Hash-Wert nicht mehr passen.
Dieses Verfahren wäre das digitale Äquivalent zur Hinterlegung von Dokumenten bei einem Notar - es wird beweisbar, daß bestimmte Dokumente zu einem bestimmten Zeitpunkt existiert haben, ohne daß die Dokumente selbst veröffentlicht werden müssen.