| Zusammenfassung zur DCT Hier nochmal die Formel der forward DCT, auch FDCT. Bei dieser Berechnung werden 8x8 Bildpunkte s(y, x) in 8x8 Koeffizienten S(v, u) transformiert. mit An der Information ändert dies nichts. In den Koeffizienten ist immer noch das gleiche Bild gespeichert, jedoch auf Grundlage einer anderen Basis. Die angegebene Formel ist dabei nichts anderes als eine gewöhnliche lineare Abbildung, genauer eine Drehung. Wie in der Übung besprochen werden die Grauwerte dabei so gedreht, dass (hoffentlich) danach die meisten Koeffizienten Null werden um möglichst einfach lauflängenkodiert zu werden. Die Drehung in die entgegengesetzte Richtung heißt inverse DCT oder IDCT und ist dabei wie folgt definiert. Dabei werden aus den Koeffizienten S(v, u) wieder Grauwerte s(y, x) erzeugt. Bemerkung: Auch bei der Wavelettransformation in der kommenden Vorlesung handelt es sich um eine Drehung. Am Beispiel des Haarwavelets ist diese Zerlegung aber intuitiver zu verstehen. Wie kommen die Faktoren C(.) zustande? In der Übung kam noch die Frage auf, wie die Vorfaktoren C(.) zustande kommen. Weil in einer Drehung per Definition Längen und Winkel erhalten bleiben müssen, muss auch jeder Basisvektor die Länge eins haben und senkrecht auf allen anderen stehen. Man kann das durch Festhalten von (v, u) mit bel. Werten nachprüfen, indem man jeden Cosinusterm cos(...)*cos(...) innerhalb der Summe für alle x, y ausrechnet und die 64 Werte in einen Spaltenvektor schreibt. Dann wählt man andere Werte für v, u und tut das gleiche. Das Produkt beider Vektoren muss Null sein, die Länge eins. Lediglich wenn u und v Null werden, wird der Ausdruck im Argument des Cosinus immer Null. Wegen cos(0)=1 hat der entsprechende Vektor 64 Einsen und somit die Länge 8. Das wird einfach durch die Vorfaktoren ausgeglichen (siehe zweite Zeile des folgenden Ausdrucks). 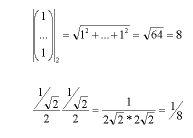 |
Beispielprogramm aus der
Übung zur DCT Unter Linux das tar-file dct_reference.tar.gz auspacken, ins Verzeichnis dct_reference wechseln und Programm (automatisch) konfigurieren, dann kompilieren. tar xzf dct_reference.tar.gz (Auspacken) cd dct_reference (Verz. wechseln) ./configure (konfigurieren) make (kompilieren) ./dct_transform (starten) Das gesamte Programm steht in dct_transform.cxx und es gibt folgende Möglichkeiten mit der Transformation zu experimentieren:
Das Programm verwendet die SDL
Bibliothek die in allen Linux Distributionen
enthalten ist und auch auf Windows portiert wurde.
Eine ausführbare Version des Programmes befindet
sich hier.
Wer Zuhause kein Linux installiert hat kann das
Programm einfach im PI-Pool (D7) testen. dct_transform.cxx kann auch ohne Änderungen unter
Windows kompiliert werden, wenn man zuvor die SDL
installiert. |