a) Implementierung eines allgemeinen Faltungsfilters

Aufgabestellung:  Die in Aufgabe 1 entworfene Bild-Klasse soll um eine Routine erweitert werden mit der eine beliebige Faltung beliebiger Groesse durchgefuehrt werden kann.

Informationen:

Mittels einer Faltungsoperation werden Bildpunkte in kleinen Nachbarschaften miteinander verknuepft. Diese Verknuepfung erfolgt durch eine Operation, die jeden Bildpunkt  innerhalb eines bestimmten Bereichs mit einem entsprechenden Gewicht multipliziert, die Produkte addiert und die Summe an eine bestimmte Position des Bildes schreibt.

Beispiel: Eine 3x3 Maske wird ueber dem rot gekennzeichneten Pixel ("Zentralpixel") positioniert, die Faltungsoperation wird durchgefuehrt und das Ergebnis wird in das Ergebnisbild an die Position des Zentralpixels eingetragen.
 

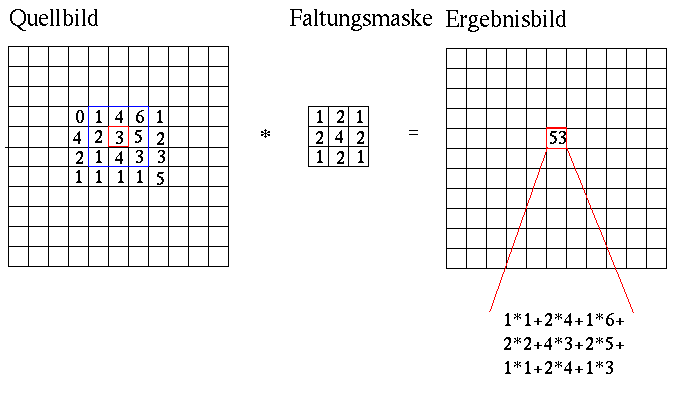
Um das gesamte Bild zu filtern wird - analog zum Beispiel -  die Faltungsoperation auf allen Bildpunkten des Quellbildes durchgefuehrt und das Ergebnis wird im Ergebnisbild abgelegt.

Am Bildrand tritt das Problem auf, dass die Faltungsmaske ueber die vorhandenen Daten hinausreicht. Dieses kann auf unterschiedliche Weise gehandhabt werden, wir gehen hier davon aus, dass sich die Randspalten bzw. -zeilen unendlich wiederholen.

RGB-Bilder, also Bilder mit mehreren Baendern, werden durch getrennte Anwendung der Faltung auf jedes Band gefiltert.

b) Anwendung verschiedener Filter

Aufgabenstellung:  Die unter a) entworfene Routine soll mit verschiedenen Filtermasken getestet werden:

1) Es soll ein 5x5-Gaussfilter auf  das Bild lenna_noise.ppm angewendet werden. Was passiert?
2) Das Bild lenna.pgm soll mit dem eindimensionalen Filter (1/2 0 -1/2) gefiltert werden? Was bewirkt der Filter?

Informationen:

zu 1) Die Gauss-Filtermaske kann fuer beliebige Groessen aus dem Pascal'schen Dreieck bestimmt werden:

                                        1
                                     1     1
                                 1      2      1
                             1      3      3      1
                         1      4      6      4       1
                       .        .    .     .   .        .         .

D.h. eine eindimensionale Gauss-Filtermaske der Groesse 3 ergibt sich zu (1 2 1).
Die zweidimensionale Gauss-Maske ergibt sich aus den eindimensionalen Masken wie folgt:
 
        1  * (1 2 1)        1  2  1
        2  * (1 2 1)   =   2 4  2
        1  * (1 2 1)        1  2  1

Um den mittleren Grauwert zu erhalten ist es weiterhin notwendig das Ergebnis jeder Faltungsoperation durch die Summe der Maskenkoeffizienten zu teilen oder die Filtermaske entsprechend zu modifizieren:

    1/16  2/16  1/16
    2/16  4/16  2/16
    1/16  2/16  1/16