Universität Mannheim
Lehrstuhl für Praktische Informatik IV
Prof. Dr. W. Effelsberg
R. Lienhart 416
S. Pfeiffer 417

Bitte unbedingt beachten:

Die Programme müssen in ANSI-C geschrieben werden.
Sie müssen im Pool mit dem GNU C-Compiler gcc -Wall -ansi -pedantic fehlerfrei übersetzbar und lauffähig sein.
Wenn mehrere Dateien mit der abox abgegeben werden sollen, müssen sie vorher mit dem Befehl tar zu einer Datei zusammengebunden werden.

Übungsblatt 7

Abgabe: 25.1.96 um 12:00 Uhr

Aufgabe 1 [40 Punkte]

  1. Gegeben sei ein gerichteter Graph in folgendem Dateiformat:

    /Anzahl der Knoten/ /Anzahl der Kanten/
    /From Knoten/ /To Knoten/
    ...
    /From Knoten/ /To Knoten/

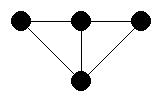
    z.B. für den (ungerichteten) Graphen in der unteren Abbildung ergibt sich:
    4 10
    1 2
    2 1
    2 3
    3 2
    3 4
    4 3
    4 1
    1 4
    4 2
    2 4

    Schreiben Sie eine Funktion, die den Graphen einliest.

  2. Schreiben Sie jeweils eine Funktion, die testet, ob der gerichtete Graph ist. Implementieren Sie auch die Breiten- und Tiefensuche. Schreiben Sie ein Hauptprogramm, in dem man die Eingabedatei für den Graphen sowie die Funktionen, die man auf rufen kann, interaktiv eingeben kann. Das Ergebnis soll auf dem Bildschirm ausgegeben werden.

Aufgabe 2 [20 Punkte]

  1. Bestimmen Sie alle Gerüste zu dem in der unteren Abbildung angegebenen Graphen. (Ein Gerüst G' eines Graphen G ist ein Graph, der dieselben Knoten wie G enthält, zusammenhängend ist und eine minimale Zahl der Kanten von G besitzt. Diese Kanten sind notwendig, damit der Graph zusammenhängend bleibt.)

  2. Beweisen Sie, daß eine Gerüst ein Spannbaum ist. Dazu müssen Sie zeigen, daß jeder minimale, zusammenhängende Graph ein Spannbaum ist.
  3. Geben Sie einen Algorithmus an, der das Minimalgerüst eines Graphen G bestimmt.
Last modified: Thu Jan 11 11:07:53 MET 1996