
Entwicklung und Implementierung einer
interaktiven AVL-Animation

Studienarbeit
von
Axel Semling
aus
Mannheim
Vorgelegt am
Lehrstuhl für Praktische Informatik IV,
Prof. Dr. W. Effelsberg
Fakultät für Mathematik und Informatik,
Universität Mannheim
Juni 1997
Betreuer:
Dipl.-Wirtsch.-Inform. Christoph Kuhmünch
Inhaltsverzeichnis
Kapitel 1
*Motivation und Aufgabenstellung
*Kapitel 2
*Die Programmiersprache Java
*Kapitel 3
*AVL-Bäume
*3.1 Definition
*3.2 Zusamennhang zwischen Knotenzahl und Baumhöhe
*3.3 Einfügen in einen AVL-Baum
*3.4 Löschen eines Schlüssels aus einem AVL-Baum
*Kapitel 4
*Benutzerführung für das Programm
*4.1 Menüleiste
*4.2 Baumoperationen
*4.3 Steuerungspanel
*4.4 Bedienungsvereinfachungen
*Kapitel 5
*Interner Programmaufbau
*5.1 Analyse und Design
*5.1.1 Art und Umfang der Darstellung
*5.1.2 Klassenbeschreibung
*5.1.3 Programmablauf
*5.1.4 Klassenhierachie
*Kapitel 6
*Ausblick
*Literaturverzeichnis
*
Abbildungsverzeichnis
Abbildung 2.1: Vom Quell- zum Maschinencode
*Abbildung 3.1: Binärbaume
*Abbildung 3.2: Fibanocci-Baum
*Abbildung 3.3: Schlüssel in einen AVL-BAum einfügen
*Abbildung 3.4: Schlüssel x wird links von Elternknoten p eingefügt
*Abbildung 3.5: Schlüssel x wird an ein Blatt angehängt
*Abbildung 3.6: p ist linker Sohn seines Elternknotens j p und bal(j p) = +1
*Abbildung 3.7: p ist linker Sohn seines Elternknotens j p und bal(j p) = 0
*Abbildung 3.8: p ist linker Sohn seines Elternknotens j p und bal(j p) = -1
*Abbildung 3.9: Rotation nach rechts
*Abbildung 3.10: Doppelrotation nach rechts
*Abbildung 3.11: p ist linker Sohn seines Elternknotens j p und bal(j p) = -1
*Abbildung 3.12: p ist linker Sohn seines Elternknotens j p und bal(j p) = 0
*Abbildung 3.13: p ist linker Sohn seines Elternknotens j p und bal(j p) = +1
*Abbildung 3.14: Rotation nach links und bal(q) = 0
*Abbildung 3.15: Rotation nach links und bal(q) = +1
*Abbildung 3.16: Doppelrotation nach links
*Abbildung 4.1: Menüleiste
*Abbildung 5.1: Hauptfenster
*Abbildung 5.2: Klassenhierarchie des Programms AVLTree
*
Das Projekt TeleTeaching der Universitäten Heidelberg und Mannheim befaßt sich mit dem gegenseitigen Austausch von Vorlesungen mittels eines digitalen Hochgeschwindig-keitsnetzes. Im Sommersemester 1996 wurde erstmals die Vorlesung Rechnernetze von Prof. Dr. Effelsberg auf diese Weise nach Heidelberg übertragen. Weitere Vorlesungübertragungen werden in Zukunft in beide Richtungen folgen.
Das Tele-Teaching hat sich zum Ziel gesetzt neue Formen des Lernens und Lehrens mit Hilfe neuer Medien zu proben und einzusetzen. Als primäre Ziele gelten die Bereicherung des Lehrangebots, Verbesserung der Lehre und Entwicklung eines Tele-Learning- Gesamtkonzepts. Die vorhandenen Lehr- und Lernmethoden sollen nicht erstetzt, sondern sinnvoll ergänzt werden.
Die erziehungswissenschaftliche Begleitung und Evaluierung durch die beteiligten Lehrstühle Erziehungswissenschaft II in Mannheim und Psychologie in Heidelberg ist von zentraler Bedeutung. So können Lern- und Akzeptanzschwierigkeiten bereits während der Entwicklung entgegengesteuert werden [EEG97].
Zu den Vorlesungen wird das Unterrichtsmaterial multimedial aufbereitet (Text, Graphiken, Video, Audio, etc.) und den Studenten per WWW zur Nachbereitung und Prüfungsvorbereitung zur Verfügung gestellt. Gegenüber klassischen Medien, wie z.B. Büchern bietet der Computer die Möglichkeit, interaktiv zu lernen, statt passiv zu konsumieren. Selbstständiges Ausprobieren und Anwenden des Wissens optimiert den Lerneffekt. Basierend auf dem "Learning by doing" – Prinzip sollten daher, zusätzlich zum reinen Vorlesungsstoff, interaktive Animationen/Simulationen entwickelt werden, die über WWW abrufbar sind.
Ziel dieser Studienarbeit ist die Entwicklung eines interaktiven Animations- bzw. Simulationsprogramms zur Visualisierung des AVL-Baum-Algorithmus, welcher in der Vorlesung Programmierverfahren und Datenstrukturen abgehandelt wird. Mit diesem Programm soll der Anwender in der Lage sein, seinen eigenen AVL-Baum nach belieben aufzubauen. Auf interaktives Eingreifen seitens der Anwender wird großes Augenmerkmal bei der Umsetzung gesetzt. Alle Aktivität geht direkt vom Benutzer aus. Damit der Lerneffekt noch zusätzlich verstärkt wird, ist ein Textfenster eingebaut. In diesem wird dem Benutzer permanent das aktuelle Geschehen klar verständlich erklärt.
Da die Animation im WWW abgelegt wird, soll das Programm auf mehreren Plattformen lauffähig sein. Aus diesem Grunde fiel die Wahl auf die an C++ angelehnte plattenformunabhängige Programmiersprache Java.
Besonderer Wert wird hierbei auf eine objektorientierte Entwicklung gelegt. Die entwickelten Basisklassen sollen so flexibel gestaltet werden, daß sie sich ohne signifikante Änderungen auch für Animationen in anderen Bereichen eignen.
Wie oben bereits erwähnt, wurde die Implemenitierung mit der Programmiersprache Java vorgenommen. Im folgenden Kapitel wird daher auf Java eingegangen. Ein wichtiger Bestandteil dieser Studienarbeit stellen AVL-Bäume dar. Sie werden im Kapitel 3 erklärt. Alle wichtige theoretische Hintegründe zu AVL-Bäumen wird in diesem Kapitel abgehandelt. Ferner wird speziell auf das Einfügen und Löschen von Knoten eingegangen. Im Kapitel 4 wird die Benutzerführung für das Programm erläutert. Alle Bedienungsmöglichkeiten werden explizit dargelegt, so daß beim Umgehen mit dem Programm keine Bedienungsfragen entstehen. Im letzten Kapitel wird das Thema Interner Programmaufbau aufgegriffen. In diesem werden Analyse und Design behandelt. Zudem wird zum Schluß auf Erweiterbarkeit und Verbesserungsvorschläge eingegangen.
Die Programmiersprache Java
Offenkundig ist Java derzeit die Programmiersprache fürs Internet. Sie bietet interessante Möglichkeiten, mit dynamischen HTML-Dokumenten Bewegung ins Web zu bringen, ohne für jede Änderung den HTTP-Server zu konsulitieren.
Java ist objektorientiert und vergleichbar mit C++, ist aber um einige Möglichkeiten ärmer. Sie ist so konzipiert, daß sie portabel ist. Die Portabilität reicht über verschiedene Plattformen und Betriebssysteme.
Normalerweise übersetzt ein Compiler Programme, die etwa in C++ geschrieben sind, in Maschinencode für einen speziellen Prozessor. Wenn das Programm auf einem anderen Rechner ablaufen soll, muß es ausgehend vom Quellcode neu kompiliert werden.
Im Gegensatz dazu enthält das Java Developers Kit (kurz JDK) zwei Arten von Übersetzern: den Java-Interpreter und den Java-Compiler. Letzterer generiert den maschinenunabhängigen Bytecode, der von ersterem und Interpretern aller anderen Plattformen abgearbeitet werden (siehe Abbildung 2.1).
Abbildung 2.1
Die Entwickler von Java haben ihre Ziele stichwortartig wie folgt zusammengefaßt:
Einfach, Objektorientiert, Verteilt, Robust, Sicher, Architekturneutral, Portabel, Interpretiert, Hohe Leistung, Multithreading und Dynamisch.
Nähere Erläuterungen zu obigen Schlägwörten findet man im Internet unter der URL-Adresse
http://java.sun.com oder in den Büchern [F96] und [CH97].Vielmehr soll es von Interesse sein, auf erste Erfahrungenswerte einzugehen, die bei dieser neuen Programmiersprache gesammelt wurden. Die Studienarbeit wurde mit der Version 1.0 von Java erstellt.
Keine Programmiersprache, die so viele Möglichkeiten bietet wie Java, ist leicht erlernbar. Man muß dabei zwischen kleinen Applets und größeren anspruchsvollen Programmen unterscheiden. Viele Java-Bücher widmen nur einen kleinen Teil ihres Inhalts der Sprache und den größten Umfang der Java-Bibliothek, welche über 150 Klassen und Schnittstellen beinhaltet. Man muß nicht alle davon für einen Programmierauftrag kennen, aber man braucht für jedes Projekt einige davon.
Etwas unübersichtlich ist der Aufbau der AWT-Bibliothek, verglichen beispielsweise mit Delphi. Auch könnte die Ereignisstruktur etwas ausgefeilter sein. Windows besitzt Hunderte von Ereignissen, Java dagegen nur knapp zwei Dutzend.
Viele Entwickler schreiben Programme am liebsten mit Hilfe spezieller Editoren. Aber PC-Programmierer, die "drag and drop" Systeme oder integrierte Entwicklungsplattformen, wie moderne C++ Compiler gewohnt sind, werden bestürzt sein. In diesem Punkt ist Besserung in Sicht, wodurch sich die Entwicklungszeit mit Java erheblich verkürzen wird.
Viele glauben, daß Java die universelle Programmiersprache für alle Programmiersprachen wird. Dies ist theoretisch möglich. Ob man sich auf den kleinsten gemeinsamen Nenner einigen wird, steht noch offen. Ein Beispiel: Man wird vergeblich versuchen die rechte Maustaste als Event aufzufangen, denn Java soll auch auf Plattformen benutzbar sein, bei denen die Mäuse nur eine Taste haben, wie dies beim Macintosh der Fall ist.
Java-Anwendungen sehen nicht so gut aus, wie etwa solche, die unter Windows-Anwendungen entwickelt wurden. Auf jeden Fall sind die mit Java 1.0 gelieferten Grafikwerkzeuge zu primitiv, um ein ansprechendes Design zu gestalten.
Die größten Probleme bei der Implementierung entstanden in der zum Teil noch fehlenden Kompatibilität. Ein fehlerloses Ablaufen unter dem Appletviewer bedeutet jedoch nicht, daß dies genauso unter einem Browser geschieht. Oft traten Securityfehler beim Ablauf des Programms unter einem Browser auf. So war es z.B. ein lang ungelöstes Rätsel, warum Securtity-Fehler beim Stoppen von Threads unter Netscape auftraten. Netscape erlaubt keine Threads, die in einer Klasse gestartet wurden, in einer anderen zu beeinflußen.
Mit Threads besteht auch das Problem der Zusammenarbeit zwischen Thread-Package und Betriebssystem. Wie ein Thread abläuft ist Sache des Betriebssystems. Nur das Betriebssystem kann die CPU-Zyklen zur Verfügung stellen. Es gibt Betriebssysteme, die einen laufenden Thread solange aktiv halten, bis ein höherwertiger Thread aktiviert wird und die Steuerung übernimmt. Andere Thread-Systeme weisen jedem laufenden Thread einen Zeitabschnitt zu, um seine Aufgabe zu erledigen. So ist es wohl auch zu erklären, weshalb das Applet unter manchen Betriebssystemen ruckartig und nicht flüssig abläuft.
Die Euphorie hinsichtlich Java ist ungebremst und wird voraussichtlich noch lange anhalten, da Java noch in seiner Entwicklungsphase steckt und noch viel Reden von sich machen wird. So kommt mit Java-Office, das in Kürze erscheinen soll, ein Produkt auf den Markt, das weitere Brücken zwischen verschiedenen Plattformen schlagen wird.
AVL-Bäume
Bäume gehören zu der wichtigsten in der Informatik auftretende Datenstruktur. Insbesonders kommen Binärbäume häufig vor. Mit ihnen können die Operationen Suchen, Einfügen und Entfernen effizient implementiert werden.
Die Operationen Suchen, Einfügen und Entfernen eines Schlüssels in einem zufällig erzeugten Binärbaum mit n Knoten ist zwar im Mittel mit der Komplexität O (log2n) durchführbar, im worst-case kann jedoch ein entarteter Binärbaum entstehen. Dieser gleicht dann einer linearen Liste, wobei zur Durchführung einer Operation ein Aufwand von O(n) entsteht.
Durch zusätzliche Bedingungen an die Struktur des Baumes kann dies verhindert werden. In der Literatur [OW96] wird eine Vielfalt von Möglichkeiten beschrieben, die die Struktur eines Baumes mit n Knoten und einer Höhe von O(log2n) zusichern und somit die Durchführung aller Baumoperationen in logarithmischer Zeit ermöglichen.
Der erste historische Vorschlag stammt von Adelson-Velskij und Landis. Eine entartete Struktur eines Binärbaumes wird durch die Forderungen an die Höhendifferenz der beiden Teilbäume eines jedes Knotens verhindert. Sie gehören deshalb auch der Klasse der höhenbalancierten Bäume an.
Bäume, die diese Bedingungen erfüllen, heißen nach ihren Schöpfern AVL-Bäume.
Im folgenden Kapitel wird zuerst die Definition von AVL-Bäumen wiedergegeben. Danach wird mit dieser der Zusammenhang zwischen Knotenzahl und Baumhöhe untersucht. Damit kann gezeigt werden, daß AVL-Bäume nie entarten. Im Anschluß werden die Operationen Einfügen eines Schlüssels in einen AVL-Baum und Entfernen eines Schlüssels aus einem AVL-Baum erläutert.
3.1 Definition
Ein binärer Suchbaum T ist AVL-ausgeglichen oder höhenbalanciert, kurz: ein AVL-Baum, wenn für jeden Knoten p des Baumes gilt, daß sich die Höhe des rechten Teilbaumes von der des linken Teilbaumes höchstens um eins unterscheidet [OW96].
| Höhe(linker Teilbaum(p)) – Höhe(rechter Teilbaum(p)) | £ 1 " p Î T
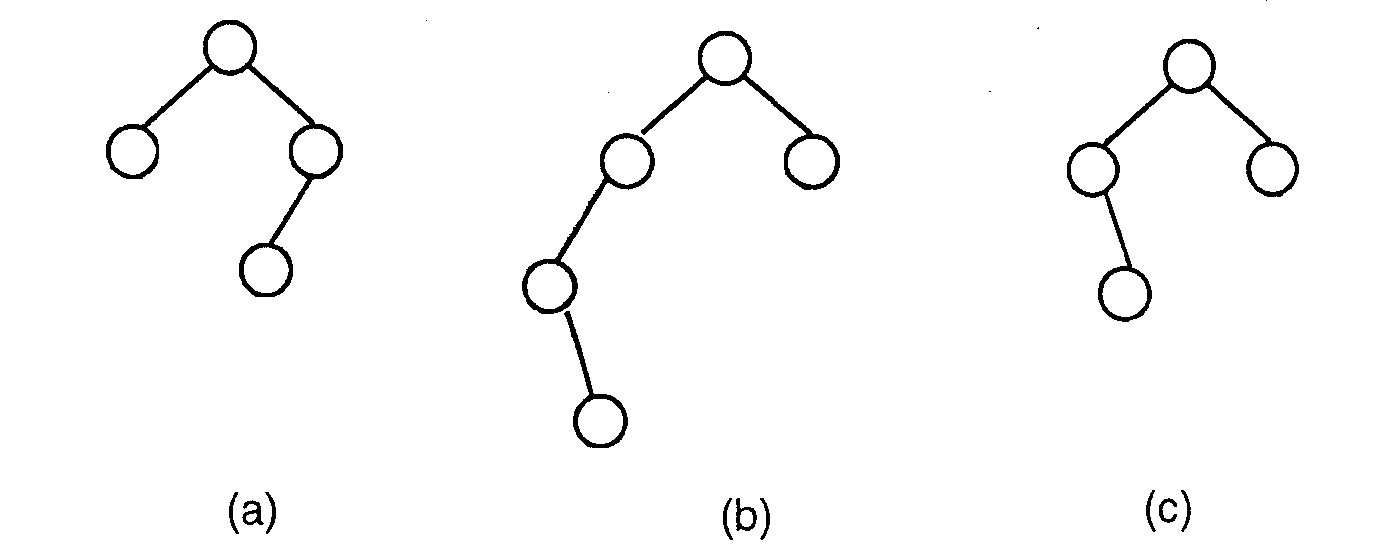
In Abbildung 3.1 sind (a) und (c) Beispiele für AVL-Bäume, (b) ist dagegen kein AVL-Baum.
Die Motivation ist, entartete Binärbaume zu verhindern. AVL-Bäume können nie zu linearen Listen entarten. Folgende Überlegung zeigt, daß AVL-Bäume mit n Knoten eine Höhe von O(log2n) haben.
a) Die maximale Höhe h für einen völlig ausgeglichenen Baum wird mit n = 2h – 1 erreicht Daraus folgt für h unmittelbar log2(n+1) –1 £ h.
b) Um die minimale Knotenzahl zu ermitteln, formuliert man folgenden induktiven Ansatz:
Ein AVL-Baum T0 mit der Höhe 0 hat mindestens ein Blatt, ein AVL-Baum T1 der Höhe 1 mindestens 2 Knoten. Um den Baum mit der Mindestknotenzahl Th h>1 zu konstruieren, müssen wir die Wurzel mit zwei Teilbäumen versehen, die wiederum eine minimale Anzahl von Knoten haben. Natürlich muß ein Teilbaum die Höhe h-1 haben, der andere kann dann eine, um eins kleinere Höhe, nämlich h-2 haben, damit die AVL-Ausgeglichenheit weitherin gegeben ist.
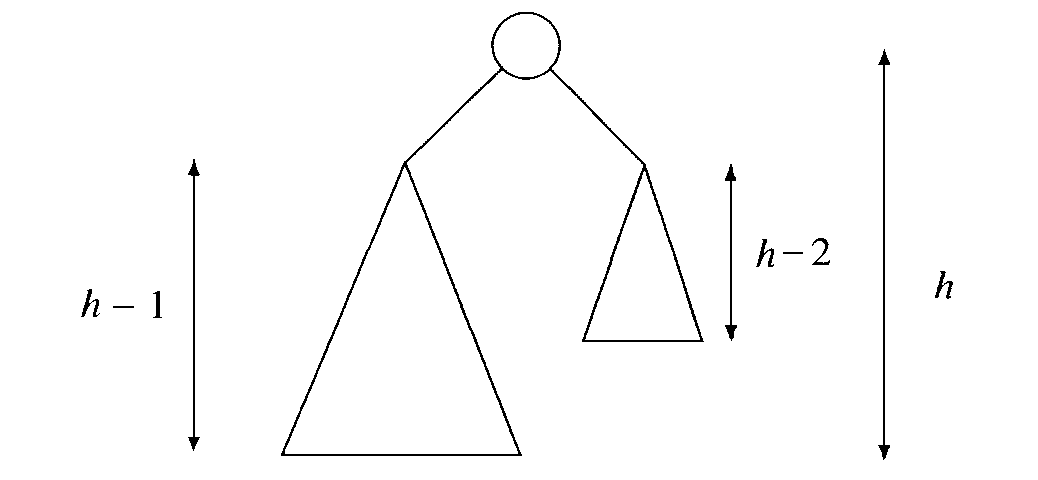 Da dieses Prinzip sehr stark dem der Fibanocci-Zahlen gleicht, heißen sie Fibanocci-Bäume (siehe Abbildung 3.2).
Da dieses Prinzip sehr stark dem der Fibanocci-Zahlen gleicht, heißen sie Fibanocci-Bäume (siehe Abbildung 3.2).
Þ Th = Th-1 + 1 + Th-2 (linker Teilbaum + Wurzel + rechter Teilbaum)
Þ (Th +1) = (Th-1 + 1) + (Th-2 + 1)
Setze nun fh º Th + 1 mit fh = fh-1 + fh-2 (Fibanocci-Zahlen).
Die minimale Knotenzahl n von Fibonacci-Bäumen beträgt damit f
h-1. Durch vollständige Induktion kann man beweisen, daß fh-1 » 1.17 * 1.618h - 1 ist [OW96].Þ n + 1 ³ 1.17 * 1.618h
Þ log2(n+1) ³ log2(1.17) + h * log2(1.618)
Þ log2(n+1) – log2(1.17) ³ h * log2(1.618)
Þ h £ (log2(n+1) – log2(1.17)) / log2(1.618) £ 1.44 * log2(n+1)
Aus a) und b) folgt: log2(n+1) –1 £ h £ 1.44 * log2(n+1) Þ AVL-Baum hat Höhe von O(log2n).
Ein AVL-Baum ist dadurch charakterisiert, daß jeder Knoten p einen Balancefaktor bal(p) mitführt, der wie folgt definiert ist:
bal(p) = Höhe rechter Teilbaum(p) – Höhe linker Teilbaum(p)
Aus der Definition eines AVL-Baums folgt: bal(p) Î {-1, 0, 1}" p Î T.
Wie später noch zu sehen ist, muß man nicht die Höhen der Teilbäume jedes Knoten kennen.
Um einen Schlüssel in einen AVL-Baum einzufügen, sucht man zunächst nach dem Schlüssel im Baum. Wenn der einzufügende Schlüssel noch nicht existiert endet die Suche in dem Blatt, an dem er angehängt wird. Nun kann es aber sein, daß dadurch keine AVL-Ausgeglichenheit mehr vorliegt.
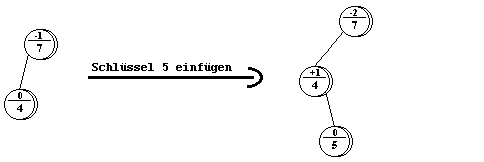
Liegt ein Fall wie in Abbildung 3.3 vor, muß die Ausgeglichenheit wieder durch eine sogenannte Rotation oder Doppelrotation hergestellt werden.
Beim Einfügen eines neuen Knoten x können die folgenden Fälle unterschieden werden:
a) Der Elternknoten von x besitzt bereits einen Sohn (siehe Abbildung 3.4).
Der Schlüssel x wird links von Elternknoten p eingefügt (siehe Abbildung 3.4). In diesem Fall verschiebt sich die Balance des Elternknotens auf 0. Da sich die Höhe des Baumes durch die Operation nicht verändert hat, muß keine Operation durchgeführt werden. Analog verhält es sich, wenn Elternknoten p bereits einen linken Sohn hat und rechts von p der neue Schlüssel x angehängt wird.
b) Der Elternknoten war vorher ein Blatt (siehe Abbildung 3.5).
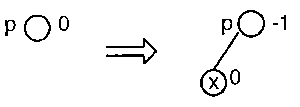
War vor dem Einfügen des Schlüssel x der Elternknoten p von x ein Blatt, so verschiebt sich die Balance des Teilbaumes mit Wurzel p in eine Richtung. Der Teilbaum mit Wurzel p ist in der Höhe um eins gewachsen. Da sich dadurch auch andere Balancefaktoren von Knoten verändern können, muß eine Prozdur upin(p) aufgerufen werden, die im folgenden erläutert wird.
c) Wenn upin(p) aufgerufen wird, so ist bal(p) Î {+1, -1} und die Höhe des Teilbaumes mit Wurzel p ist in der Höhe um eins gewachsen. Man muß darauf achten, daß vor jedem Aufruf von upin(p) diese Invariante gilt. Die Prozedur upin(p) bricht ab, falls p keinen Vater hat, d.h. wenn p die Wurzel des Baumes ist.
Man unterscheidet zwei Fälle, je nachdem ob p linker oder rechter Sohn seines Elternkotens j p ist.
Fall 1 [p ist linker Sohn seines Elternknotens j p]
Fall 1.1 [bal(j p) = +1]
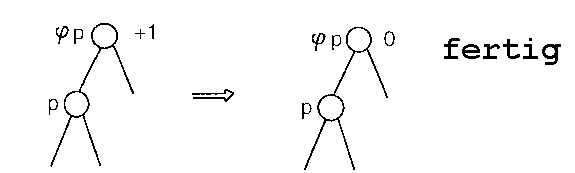
Wie in Abbildung 3.6 ersichtlich ist, hat sich Gesamthöhe des Teilbaums von j p nicht verändert. Der rechte Teilbaum von j p war bisher um eins höher als der linke. Durch den neuen Knoten im linken Teilbaum ist dieser in der Höhen um eins gewachsen. Dadurch ist der Baum mit Wurzel j p nun ausbalanciert. Weitere Untersuchungen sind nicht mehr notwendig. Alle Balancefaktoren der Knoten, die sich noch auf dem Suchpfad zur Wurzel befinden, können sich nun nicht mehr verändern, weil alle Teilbaumhöhen dieser Knoten gleich geblieben sind.
Fall 1.2 [bal(j p) = 0]
In diesem Fall verschiebt sich die Balance des Elternknotens j p auf -1 (siehe Abbildung 3.7). Vor dem Einfügevorgang war der Teilbaum mit Wurzel j p ausgeglichen. Durch das Einfügen hat sich die linke Teilbaumhöhe um eins erhöht. Es gilt die Invariante, deshalb wird die Prozedur upin(j p) aufgerufen.
 Fall 1.3 [bal(j
p) = -1]
Fall 1.3 [bal(j
p) = -1]
Die Invariante sagt, daß der Teilbaum mit der Wurzel p in der Höhe um eins gewachsen ist. Aus der Voraussetzung bal(j p) = -1 kann man in diesem Fall schließen, daß bereits vor dem Einfügen des neuen Schlüssels in den linken Teilbaum von j p mit Wurzel p dieser Teilbaum eine um eins größere Höhe hatte als der rechte Teilbaum von j p. Da der Teilbaum mit der Wurzel p in der Höhe um eins gewachsen ist, ist die AVL-Ausgeglichenheit bei j p verletzt (siehe Abbildung 3.8). Wir müssen also umstrukturieren und unterscheiden dazu zwei Fälle, je nachdem ob bal(p) = +1 oder bal(j p) = -1 ist. Wegen der Invariante ist bal(p) = 0 nicht möglich.
Fall 1.3.1 [bal(p)=-1]
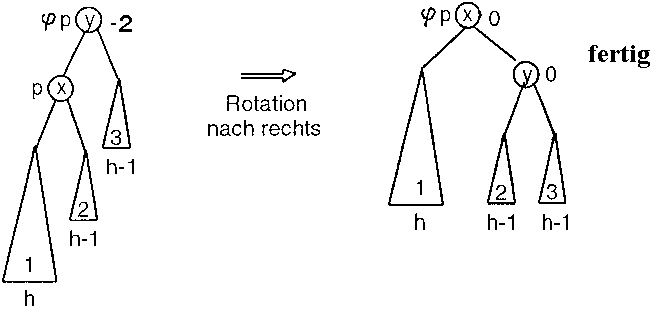
Man beachte: Nach Voraussetzung ist die Höhe des Teilbaum p um eins gewachsen und der linke Teilbaum von p um eins höher als der rechte. Eine Rotation nach rechts bringt den Baum bei j p wieder in die Balance (siehe Abbildung 3.10). Es ist keine weitere Umstrukturierung nötig, weil der durch die Rotation entstehende Teilbaum mit Wurzel j p in der Höhe nicht mehr gewachsen ist. An der Höhe der Teilbäume 1 bis 3 kann man erkennen, daß der entstandene Teilbaum nach der Umstrukturierung wieder ausgeglichen ist.
Fall 1.3.2 [bal(p) = +1]
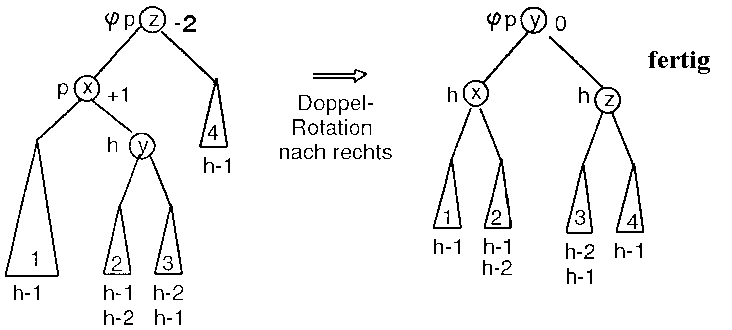
Wie in Abbildung 3.11 ersichtlich ist, sind die einzig möglichen Höhenkombinationen für die Teilbäume 2 und 3 (h-1, h-2) und (h-2, h-1). Sie können nicht die gleiche Höhe haben. Denn auf Grund der Invariante ist der Teilbaum mit Wurzel p in der Höhe um 1 gewachsen und wegen Annahme von Fall 1.3.2 ist der rechte Teilbaum von p um 1 höher als sein linker. Eine Doppelrotation nach rechts, d.h. zunächst eine Rotation nach links bei p und dann eine Rotation nach rechts bei j p, stellt die AVL-Ausgeglichenheit bei j p wieder her. Eine weitere Umstrukturierung ist nicht nötig, da der Teilbaum mit Wurzel j p in der Höhe nicht gewachsen ist.
Fall 2 [p ist rechter Sohn seines Elternknotens j p]
In diesem Fall geht man völlig analog vor und gleicht den Baum, wenn nötig, durch eine Rotation nach links bzw. eine Doppelrotation rechts-links bei j p wieder aus.
Beim Verfahren Einfügen kann im worst-case für das sukzessives Zurückgehen auf dem Suchpfad von der Einfügestelle zur Wurzel der Besuch aller Knoten erforderlich sein. Daraus folgt, daß O(log2n) Schritte, wegen logarithmischer Höhe des AVL-Baums. Dabei wird noch höchstens ein weiterer Schritt für eine Rotation oder Doppelrotation ausgeführt. Damit ist klar, daß das Einfügen eines neuen Schlüssels in einen AVL-Baum mit n Schlüsseln in O(log2n) Schritten ausführbar ist.
Um einen Schlüssel aus einen AVL-Baum zu entfernen, sucht man zunächst nach dem Schlüssel im Baum. Wenn dieser Schlüssel nicht existiert, ist das Löschen bereits beendet. Andernfalls wird der Schlüssel wie in einem Suchbaum entfernt. Nun kann es aber sein, daß anschließend keine AVL-Ausgeglichenheit mehr gegeben ist.
Beim Löschen eines Kotens können folgende Falle unterschieden werden:
Fall 1: Der zu entfernende Schlüssel ist der Schlüssel eines Knotens, dessen beide Söhne Blätter sind. Dann entfernt man den Knoten und ersetzt ihn durch ein Blatt. Falls der Baum nunmehr nicht der leere Baum geworden ist, muß für den Elternknoten p des neuen Blattes mindestens der Balancefaktor geändert werden. Falls die Balance auf bal(p) = 0 geändert werden muß, ist der Teilbaum mit Wurzel p auch in der Höhe um eins gefallen. Damit können sich auch für alle Knoten auf dem Suchpfad nach p die Balancefaktoren und die Höhen der Teilbäume verändert haben. Wir rufen daher eine Prozedur output(p) auf, die die AVL-Ausgeglichenheit wiederherstellt.
Fall 2: Der zu entfernende Schlüssel ist der Schlüssel eines Knotens p, der nur einen inneren Knoten q als Sohn hat. Dann müssen beide Söhne von q Blätter sein. Man ersetzt also den Schlüssel von p durch den Schlüssel von q und q durch ein Blatt. Damit ist nunmehr p ein Knoten mit pal(p) = 0 und die Höhe des Teilbaums mit der Wurzel p um eins gesunken. Auch in diesem Fall ruft man output(p) auf, um die AVL-Ausgeglichenheit wiederherzustellen.
Fall 3: Liegt der Fall vor, daß der zu entfernende Knoten p zwei Söhne hat, geht man wie bei natürlichen Suchbäumen vor und ersetzt den Schlüssel p durch den Schlüssel des symmetrischen Nachfolgers (oder Vorgängers), d.h. man sucht im linken (rechten) Teilbaum mit Wurzel p das größtes Element smax (kleinstes Element s
min). Vertausche die Schlüssel p und smax (smin). Der Schlüssel p muß dann ein Knoten sein, dessen Schlüssel wie in Fall 1 und 2 beschrieben entfernt wird.In jedem Fall hat man das Löschen auf die Ausführung der Prozedur output(p) für einen Knoten p mit bal(p) = 0 reduziert, dessen Teilbaum in der Höhe um eins gesunken ist.
Die Prozedur output(p) wird längs des Suchpfades rekursiv aufgerufen. Sie adjustiert die Höhenbalancen und führt gegebenfalls Rotationen oder Doppelrotationen durch. Wenn output(p) aufgerufen wird, gilt bal(p) = 0 und der Teilbaum it Wurzel p ist in der Höhe um eins gefallen. Man muß darauf achten, daß vor jedem Aufruf diese Invariante gilt. Man unterscheidet wieder zwei Fälle, je nachdem ob p linker oder rechter Sohn eines Elternknotens j p ist.
Fall 1 [p ist linker Sohn seines Elternknotens j p]
Fall 1.1 [bal(j p) = -1 ]
Die Höhe des Teilbaums mit der Wurzel j p hat sich um 1 verringert (siehe Abbildung 3.12). Damit können sich für alle Knoten auf dem Suchpfad nach die Balancefaktoren und die Höhen der Teilbäume verändert haben. Infolgedessen ruft output(j p) auf.
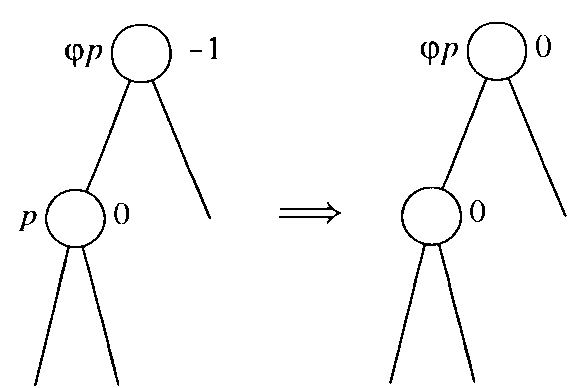
Fall 1.2 [bal(j p) = 0]
Der linke Teilbaum von Knoten j p hat sich in der Höhe um 1 verringert (siehe Abbildung 3.13). Die Höhe des Teilbaums mit Wurzel j p bleibt aber unverändert. Damit sind keine weitere Umtstrukturierungen notwendig.
Fall 1.3: [bal(j p) = +1]
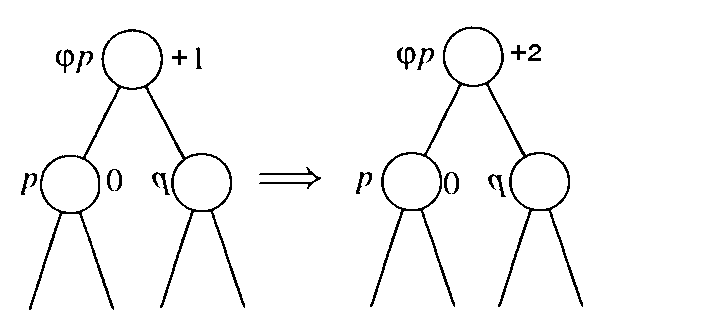
Der rechte Teilbaum von j p mit Wurzel q ist höher als der linke mit Wurzel p, der darüber hinaus noch in der Höhe um eins gefallen ist (siehe Abbildung 3.14). Wir machen eine Fallunterscheidung nach dem Balancefaktor von q.
Fall 1.3.1 [bal(q) = 0]
Durch Rotation nach links kann der Baum wieder ausgeglichen werden (siehe Abbildung 3.15). Zwar ist der linke Teilbaum von w nun um eins höher als der rechte, allerdings hat sich dadurch die Teilbaumhöhe nicht verändert. Alle Balancefaktoren der Knoten, die sich noch auf dem Suchpfad zur Wurzel befinden, können sich nun nicht mehr verändern, weil alle Teilbaumhöhen dieser Knoten gleich geblieben sind.
Fall 1.3.2 [bal(q) = +1]
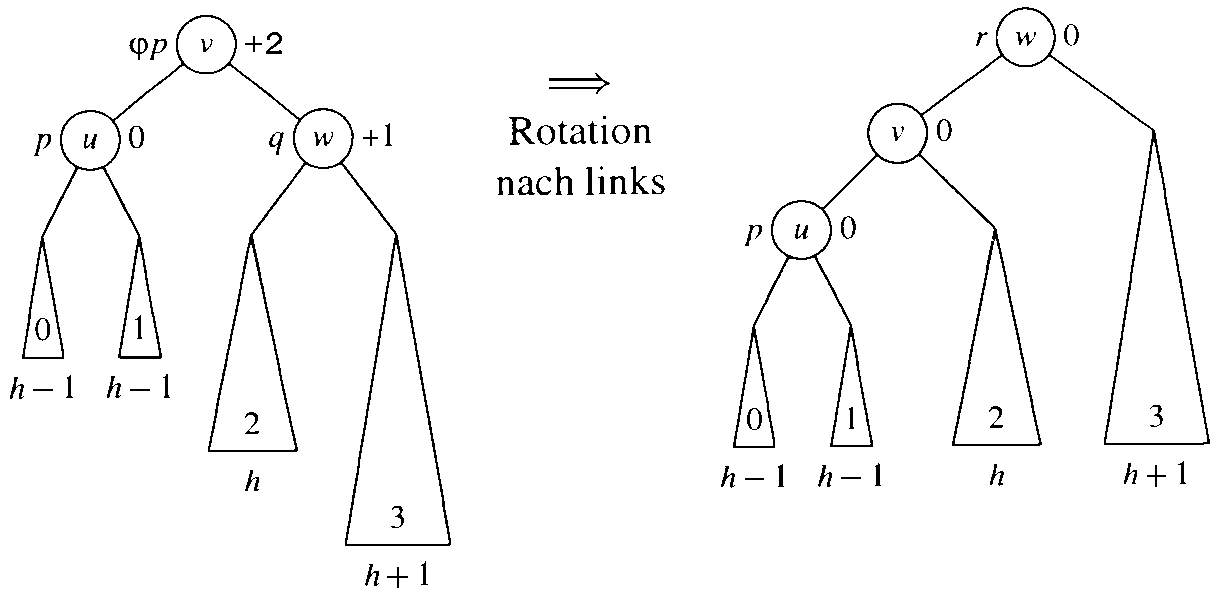
Es muß eine Rotation nach links durchgeführt werden, wie in Abbildung 3.16 dargestellt ist, um die AVL-Ausgeglichenheit wieder herzustellen. Nach der Voraussetzung hat der linke Teilbaum von q die Höhe h und ist damit um eins kleiner als der rechte. Durch die Rotation hat nun Teilbaum v einen linken und rechten Teilbaum mit Höhe h. Der Teilbaum mit Wurzel r besteht aus Teilbäumen mit den Höhen h+1 und ist damit auch ausgeglichen. Es gilt die Invariante bal(r) = 0, d.h. der linke Teilbaum hat sich in der Höhe um eins veringert. Infolgedessen wird die Prozedur output(r) aufgerufen.
Fall 1.3.3 [bal(q) = -1]
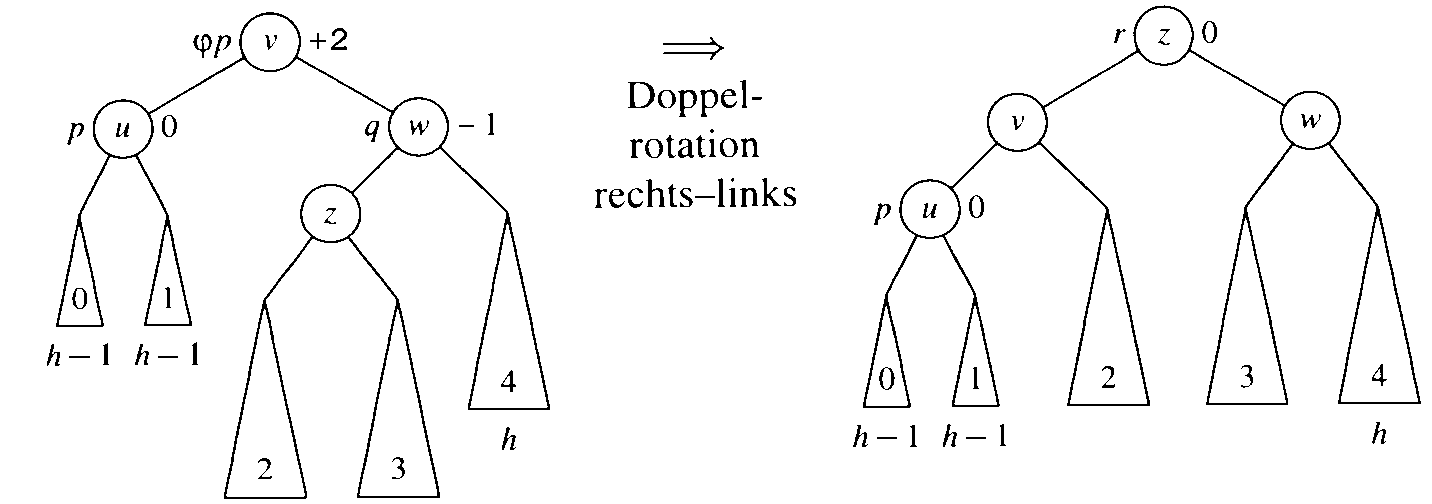
Weil der Teilbaum mit Wurzel p in der Höhe um 1 gefallen ist und der rechte Teilbaum von j p vor dem Entfernen eines Schlüssels aus dem Teilbaum mit Wurzel p um 1 höher war als der linke, folgt, daß der Teilbaum Wurzel q die Höhe h+2 haben muß. Wegen bal(q) = -1 hat der linke Teilbaum von q mit Wurzel z die Höhe h+1 und der rechte die Höhe h. Die Teilbäume von z können entweder beide Höhe h oder höchstens einer von ihnen die Höhe h-1 haben. In jedem Fall gleicht die angegebene Umstrukturierung (siehe Abbildung 3.17) den Baum wieder aus. Dabei hängen die Balancefaktoren der Knoten v und w vom Balancefaktor z ab. Auf jeden Fall hat der Teilbaum mit Wurzel r den Balancefaktor 0 und seine Höhe ist um eins gefallen. Es gilt also die Invariante für den Aufruf von output(r).
Fall 2 [p ist rechter Sohn seines Elternknotens j p]
Fall 2 ist völlig symmetrisch zum Fall 1 und wird daher nicht näher behandelt.
Ein wesentlicher Unterschied zwischen Einfügen und Löschen darf nicht übersehen werden. Während das Einfügen eines Schlüssels höchstens eine Rotation (von zwei oder drei Knoten) erfordert, kann das Löschen eine Rotation für jeden Knoten entlang des Suchpfads verursachen. Man betrachte z.B. das Löschen des Knotens mit größtem Schlüssel in einem Fibonacci-Baum. Da jedoch der Aufwand zum Ausführen einer einzelnen Rotation oder Doppelrotation konstant ist, und die Höhe h von AVL-Bäumen mit n Schlüsseln durch 1.44log2n beschränkt ist, folgt unmittelbar: Das Entfernen ist in O(log2n) Schritten möglich.
Die drei Operationen Suchen, Einfügen und Löschen sind somit im worst case in O(log2n) Schritten ausführbar. Damit sind AVL-Bäume also eine worst-case-effiziente Implementation im Gegensatz zu natürlichen Binärbäumen, die im average-case zwar genauso effizient sind, im worst case aber W (n) Schritte zum Ausführen der drei Grundoperationen benötigen.
Benutzerführung für das Programm
Da es sich bei dem Programm um eine interaktive AVL-Baum-Animation handelt, müssen dementsprechende Steuerungselemente vorhanden sein. In der Menüleiste werden Optionen angeboten, die das Programm allgemein betreffen. Die Baumoperationen Einfügen und Löschen werden im Panel Baumoperationen, rechts oben im Hauptfenster, abgehandelt. Damit die Animation besser verfolgbar ist, befindet sich unter dem Animationsfenster ein Steuerungspanel, mit dem der Animationsablauf besser verfolgbar ist. Zudem gibt es noch zwei Bedienungsvereinfachungen, die im Animationsfenster anwenbar sind und im Folgenden noch erläutert werden.
4.1 Menüleiste
Mit dem Menü Bearbeiten sind folgende Optionen gegeben:
· Ungeschehen
Die letzte Baumoperation (Löschen oder Einfügen), die durchgeführt wurde, kann rückgängig gemacht werden. Alle Aktionen des aktuellen AVL-Baums werden gespeichert. So ist es auch möglich, alle durchgeführten Ereignisse ungeschehen zu machen. Diese Option ist nur wählbar, wenn ein Baum im Animationsfenster vorhanden ist.
· Geschwindigkeit
Da das Programm auf verschiedenen Plattformen funktioniert, läuft es zwangsläufig auf Computern mit stark unterschiedlicher Performance ab. Aus diesem Grund wurde diese Option eingefügt. Dadurch ist gewährleistet, daß die Animation einerseits nicht ruckartig und andererseits viel zu schnell abläuft. Bei einer Animationsbewegung wird zwischen jeder Bewegung eine Pause gemacht, in der das Programm ruht. Nach Wahl dieser Option wird ein Fenster geöffnet, in welchem diese Pause reguliert werden kann. Je kürzer die Pause gewählt wird, desto schneller läuft die Animation.
· AVL-Baum
w Demo starten
Dem Anwender wird die Animation vorgeführt. Dabei werden automatisch vom Programm in einen AVL-Baum bestimmte Schlüssel eingefügt und gelöscht. Die Schlüssel wurden so gewählt, daß interessante Fälle dem Anwender veranschaulicht werden können. Im Eingabefenster wird dabei angegeben, welche Zahl im Baum eingefügt bzw. gelöscht wird. Die Simulation kann während des Ablaufs nicht unterbrochen werden.
w Neu
Der aktuelle AVL-Baum im Animationsfenster wird gelöscht und ein leerer AVL-Baum neu angelegt. Danach ist das Animationsfenster leer. Diese Option ist endgültig, kann also nicht mehr ungeschehen gemacht werden.
Im Menü Hilfe werden, wie im diesem Abschnitt, alle Menü- und Steuerungsoptionen erläutert. Nach Wahl einer der oben genannten Optionen, wird das Hilfe-Fenster geöffnet. Dieses Fenster ist in drei horizontale Panel (Auswahl, Infofenster und Button) eingeteilt. Im Panel Auswahl steht die ausgewählte Menü- oder Steuerungsoption, welche im Infofenster erklärt wird. Beim Aufruf der Option Hilfe, werden alle Erläuterungen im Infofenster angezeigt.
Im Panel Auswahl können auch alle Hilfe-Optionen ausgewählt werden.
Das Menü Fenster enthält nur die Option Schliessen, mit der das Hauptfenster geschlossen wird. Bei allen Fenstern, die vom Programm geöffnet werden, stehen selbstverständlich die gewohnten Bedienungstechniken für Fenster, wie z.B. vergrößern, zu Verfügung.
Im Hauptfenster befindet sich das Panel Baumoperationen. Es gibt dem Anwender die Kontrolle über den AVL-Baum. Die Operationen Schlüssel in einen AVL-Baum einfügen und löschen können hier durchgeführt werden. Dadurch ist der Anwender in der Lage, seinen eigenen AVL-Baum nach belieben aufzubauen.
Der Wertebereich der Schlüssel, die eingefügt werden können, ist beschränkt. Natürliche Zahlen zwischen 0 und 999 können sich im Binärbaum befinden. Gelöscht werden können nur solche Zahlen, die sich im aktuellen Binärbaum befinden.
Bevor eine Baumoperation durchgeführt werden kann, muß im Textfeld eine Zahl angegeben werden. Dies kann durch Benutzung des Ziffernblocks über dem Textfeld mit der Maus geschehen.
Die Eingabe kann auch über die Tastatur erfolgen. Anschließend muß diejenige Operation gewählt werden, die erfolgen soll. Wieder kann sie auf zweierlei Weise geschehen. Zum einen kann durch Anklicken der Buttons ‘Schluessel einfuegen’ und ‘Schluessel loeschen’ die gewünschte Aktion gestartet werden, zum anderen durch Drücken der Tasten ‘Enter’ (Þ Einfügen) und ‘Entf’ (Þ Löschen). Es gibt noch eine dritte Möglichkeit einen Schlüssel aus einem Binärbaum zu entfernen (siehe Bedienungsvereinfachungen).
Editieren ist im Textfeld nicht möglich. Dafür besteht die Möglichkeit, durch Aktivieren des Buttons ‘Clear’, das Textfeld nach einer Falscheingabe zu löschen
Alle Eingaben werden überprüft. Wird versucht, ein Element in den AVL-Baum einzugfügen, welches bereits im Baum existiert, wird dies ignoriert. Zusätzlich wird im Infofenster des Hauptfensters eine entsprechende Meldung ausgegeben. Analoges geschieht beim Versuch, einen Schlüssel aus dem Baum zu löschen, der sich nicht im AVL-Baum befindet.
Dieses Panel befindet sich unter dem Animationsfenster des Hauptfensters und umfaßt die Buttons ‘Stop‘, ‘Run‘ und ‘Next Step‘.
Besonderes Merkmal jeder Animation bzw. Simulation ist es, einen Sachverhalt zu visualisieren.. Nachteil ist dabei oft, daß keine Möglichkeit besteht, Einfluß auf den Ablauf zu nehmen, z.B. die Animation zu stoppen. Dem galt es entgegenzuwirken. Die Motivation war dabei hauptsächlich, dem Anwender ein Instrument in die Hand zu geben, um interessante Stellen der Animation, z.B. Rechts/Linksrotation, genau verfolgen zu können. So ist ein besserer Lerneffekt gegeben.
Beim Start einer Animation sind immer die Buttons ‘Stop‘ und ‘Next Step‘ aktiv und ‘Run‘ inaktiv. Dieser Zustand (Run) der Animation bedeutet, daß sukzessive Grafiken im Animationfenster aufgebaut werden. So entsteht der Eindruck einer Bewegung.
Wird ‘Stop‘ oder ‘Next Step‘ angeklickt, so hat dies auf die Animation die gleiche Wirkung. Die Animation wird angehalten und ruht, d.h. es werden keine weiteren Grafiken im Animationsfenster aufgebaut. Die letzte Grafik, die im Animationsfenster vor dem Stop aufgebaut war, ist sichtbar.
Nun sind die Buttons ‘Run‘ und ‘Next Step‘ aktiv und ‘Stop‘ inaktiv. Dies ist der zweite mögliche Zustand eines Animationsablaufs (Sleep).
‘Run‘ bewirkt nun, daß die Animation wieder in den Zustand Run zurückkehrt und die Animation weiterläuft. Wird dagegen ‘Next Step‘ angeglickt, wird die nächste Grafik der Bewegung im Animationsfenster aufgebaut und die Animation verweilt wieder in dem Zustand Sleep.
So kann jeder Schritt der Animation exakt verfolgt werden. Dies ist deshalb so wichtig, weil neben der Bewegung im Animationfenster gleichzeitig ausführliche Erläuterungen im Infofenster angegeben werden, welche beschreiben, was im Animationsfenster geschieht. So sind alle Aktionen für den Benutzer leicht nachvollziehbar.
Es gibt noch zwei weitere Bedienungsmöglichkeiten, um die Anwendung zu vereinfachen.
Immer wenn sich der Mauszeiger im Animationsfenster über einen Knoten im AVL-Baum befindet, wird dieser durch die Farbe Blau hervorgehoben. Dies zeigt an, daß folgende zwei Optionen ausgeführt werden können.
Es ist oft für den Benutzer von Interesse zu wissen, welche Aktionen durchgeführt werden, wenn ein neuer Knoten an einer bestimmten Stelle des Baumes neu eingefügt wird. Besteht dieser Wunsch kann dies zwar durch "Nachrechnen" herausgefunden werden. Einfacher geschieht dies jedoch durch einfaches Anklicken des Knoten (kein innerer Knoten), an dem das neue Blatt angehängt werden soll. Im Infofenster werden daraufhin potentielle Kandidaten angezeigt, die dort im Falle eines Einfügens hinwandern und links oder rechts angehängt werden.
Nicht immer kann diese Option wahrgenommen werden, weil der Wertebereich auf die natürlichen Zahlen zwischen 0 und 999 begrenzt ist, so kann z. B. kein neues Blatt links vom Knoten mit Schlüssel 0 eingefügt werden.
Vereinfacht wurde auch der Vorgang Löschen eines Knotens aus dem Binärbaum. Dem Benutzer wird die Eingabe des Schlüssels abgenommen. Wenn der gewünschte Knoten mit Doppelklick markiert wird, erscheint im Infofenster die Warnung: "Loesche Schluessel x. Bestätigung mit <Schluessel loeschen>." Wird die Meldung mit entsprechendem Button bestätigt, wird der Löschvorgang gestartet. Andernfalls kann der Vorgang durch Anklicken von ‘Clear‘ abgebrochen werden.
Interner Programmaufbau
Nach dem klassischen ‘Wasserfallmodell‘ von Boehm [KS96] wird der Prozeß der Softwareentwicklung in die Phasen Analyse, Design, Implementierung, Test und Wartung unterteilt. Ziel der Analyse ist es, ein vollständiges, konsistentes und logisches Ist-Modell des für die Softwareentwicklung relevanten Realweltausschnittes zu erstellen. Zu diesem Zweck existieren in der Literatur diverse Modelle, die unabhängig von der später verwendeten Programmiersprache Notationen zur Verfügung stellen. Bei dieser Studienarbeit wurde die objektorientierte Methode von Coad und Yourdon [CY92] gewählt, um Analyse und Design durchzuführen. Das Design ist dabei die Erweiterung der Analyse um lösungsspezifische Komponenten und ist nicht mehr von der Programmiersprache unabhängig. In der Implementierungsphase werden die Ergebnisse aus Analyse und Design in die Konstrukte der verwendeten Programmiersprache umgesetzt. Als Test wird die Überprüfung der Korrektheit und Funktionalität des Programms bezeichnet. Die Wartung steht für alle Änderungen am Programm, die nach Fertigstellung notwendig werden.
5.1 Analyse und Design
Standardvoraussetzung für die Analyse einer Aufgabenstellung ist die Erstellung einer Beschreibung des relevanten Realweltausschnittes bzw. eines Anforderungskatalogs.
Zielsetzung war die Erstellung einer interaktiven Animation, welche die Funktionsweise eines AVL-Baums simuliert. Es sollten die vier verschiedenen Baumstrukturoperationen Links-, Rechts- Links/Rechts- und Rechts/Links-Rotation möglichst klar veranschaulicht werden. Dabei sollten alle Aktionen aktiv vom Anwender ausgehen, d.h. er sollte bestimmen können, welche Schlüssel in den AVL-Baum eingefügt bzw. aus dem AVL-Baum entfernt werden. Die theoretischen Grundlage sollte nicht vollständig durch die Animation ersetzt werden. Deshalb war vorgesehen, alle wichtige Aktionen zu erläutern, da es auch einer der Hautpziele war, einen Lerneffekt bei der Benutzung des Applets zu erzielen. Um der Gefahr entgegenzuwirken, daß der Anwender durch die gleichzeitige optische Veranschaulichung und Ausgabe von Erklärungen überfordert wird, erschien es wünschenswert eine Möglichkeit einzubauen, mit welcher der Anwender einen Operationsvorgang stoppen bzw. schrittweise verfolgen kann.
Aus obigen Anforderung ergab sich die Überlegung ein Layout anzulegen, welches aus vier Panels besteht:
Diese Panels sollten ursprünglich in einem Applet aufgebaut werden und dann in eine HTML-Seite eingebunden werden, d.h. alle Panels hätten sich im Ausgabefenster eines Browsers befunden. Diese Idee wurde bald verworfen. Bei der Einbindung eines Applets in eine Web-Seite müssen die HTML-Parameter WIDTH und HEIGHT angegeben werden. Diese Parameter sind nicht optional und geben, gemessen in Bildpunkten, die Breite und Höhe des Applets an. Man muß sich daher vorher genau im Klaren darüber sein, wieviel Platz das Applet in Anspruch nehmen kann, damit es für alle Anwender gut zu sehen ist. Da aber die Anwender unterschiedliche Bildschirmauflösungen haben, war es schwer, einen zufriedenstellenden Kompromiß zwischen Größe und Übersichtlichkeit zu finden. Aus diesem Grunde wurde der Vorschlag gewählt, ein separates Hauptfenster zu definieren, siehe Abbildung 5.1. Dieses wird dann vom Applet nach der Einbettung in die Web-Seite automatisch aufgerufen. Nun ist der Benutzer in der Lage, seine optimale Fenstergröße selbst zu regulieren. Ein weiterer Grund für die Hauptfensterlösung war die Tatsache, daß ein Applet innerhalb einer Web-Seite kein Menü haben kann. Mit diesem war es dann möglich, die Optionen der Bedienung übersichtlicher und komfortabler zu gestalten.
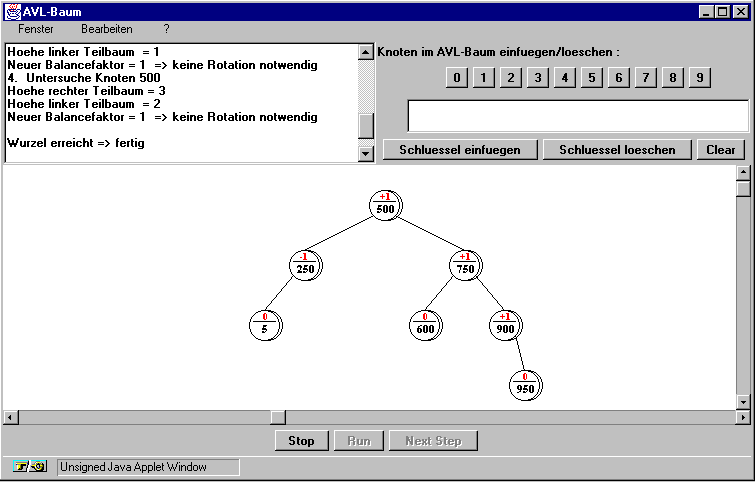
Im Animationsfenster läuft die Animation ab bzw. wird der aktuelle AVL-Baum dargestellt. Wird eine Baumoperation vom Anwender durchgeführt, wird diese im Animationsfenster optisch veranschaulicht. Beim Einfügen wächst der AVL-Baum schnell bzgl. Breite und Höhe. Demzufolge ist das Panel Animationsfenster das einzige, das mit der Größe des Haupfensters mitwächst, d.h. die Größe des Animationsfensters ist abhängig von der des Hauptfensters. Beim Vergrößern oder Verkleinern des Hauptfenster bleiben die anderen Panels in ihrer Größe unverändert.
Aufgrund der Komplexität, die sich aus dem Animationsfenster ergab, z.B. Scrollbartechnik, Double-Buffering, automatische Verschiebung der Srollbars, wurde dazu eine Klasse angelegt, die ScrollableCanvas heißt und noch im Kapitel 5 näher erläutert wird.
Die Schnittstelle zur interaktiven Animation ist das Bedienungspanel. Die Eingaben des Anwenders können per Maus oder mit der Tastatur erfolgen. Diese ausgelösten Ereignisse werden in der Prodezur handelEvent abgefangen.
Beim Infofenster handelt es sich um eine Textarea, die aus der AWT-Bibliothek übernommen wurde. Gelangt die Animation an eine wichtige Stelle, wird im Infofenster gleichzeitig ausgegeben was momentan geschieht. Durch die Scrollbars der Textarea ist es möglich, nach Animationsende nochmals Schritt für Schritt das Ergebnis der Baumoperation nachzulesen.
Im Infofenster werden zugleich Informationen zu Bedienungsanleitung angegeben und auf Fehler des Anwenders hingewiesen. So wird z.B. die Meldung ‘Element bereits vorhanden‘ eingeblendet, falls versucht wird, einen Schlüssel in einen AVL-Baum einzufügen, der dieses Element schon beeinhaltet.
5.1.1 Art und Umfang der Darstellung
Die Anwort auf die Frage nach Art und Umfang der Darstellung stellte sich als eine recht schwierige heraus. Auf welcher Abstraktionsebene sollten Daten dargestellt werden. Um so höher der Detaillierungsgrad wurde, desto schwieriger wurde eine Darstellung.
Aus diesem Grund sollten Knoten durch einen Kreis mit einem seitlich angehefteten Bogen dargestellt werden, so daß der Eindruck eines Zylinders entsteht. Die Position des Balancefaktors war im oberen Drittel des Knotens in roter Farbe vorgesehen. Darunter sollte der Schlüssel in schwarzer Farbe sichtbar sein. Zusätzlich sollten Blancefaktor und Schlüssel durch eine horizontale Linie optisch getrennt werden. Verbindungen zwischen den einzelnen Knoten wurden durch eine durchgezogene Linie dargestellt.
Das Einfügen sollte folgendermaßen vor sich gehen: Ein neuer Knoten läuft von oben ins Animationsfenster hin zur Wurzel. Von dort wandert er entsprechend der Einfügeregel von Knoten zu Knoten, bis er ein Blatt erreicht, an welches er angehängt wird. Da danach der Einfügepfad vom eingefügten Knoten bis zur Wurzel zurückverfolgt werden muß, soll der neue Knoten beim Einfügen eine dicke blaue Linie hinter sich herziehen. Dementsprechend soll sich diese blaue Linie beim Zurückverfolgen des Einfügepfads wieder auflösen. Bei jedem Knoten, der erreicht wird, erfolgt eine Untersuchung, deren Ergebnis im Infofenster ausgegeben wird. Ist eine Rotation erforderlich, wird der aktuelle Baum durch eine unauffällige graue Farbe im Hintergrund gezeichnet. Alle Knoten, die in die Rotation involviert sind, bewegen sich zu ihrem Bestimmungsort. Dabei kommen alle Knoten, obwohl sie Wege mit unterschiedliche Länge haben, gleichzeitig am Bestimmungsort an, was bedeutet, daß sie sich zum Teil mit unterschiedlicher Geschwindigkeit bewegen.
Über den Knoten, um den die Rotation vollzogen wird, soll zur Verdeutlichung ein blauer Pfeil gezeichnet werden, der die Richtung der Rotation anzeigt. Nach Ende der Rotation wird der aktuelle AVL-Baum wieder in üblichen Art dargestellt.
Das Löschen eines Knotens sollte sich analog zum Einfügen vollziehen. Komplexer ist das Löschen als das Einfügen. Zuerst muß der zu löschende Schlüssel gesucht werden, was durch eine von Knoten zu Knoten laufende blaue dicke Linie in der Animation dargestellt wird. Handelt es sich bei dem gefundnen Knoten um einen inneren, muß dieser zuerst noch mit einem Blatt vertauscht werden. Dies wird in der Animation wie bei der Rotation dargestellt, wobei dabei kein Pfeil gezeichnet wird. Ab diesem Zeitpunkt geht es analog dem Einfügen weiter.
Ein weiteres Problem enstand während der Implementierung. Der aktuelle AVL-Baum kann sehr groß werden, so daß er nur teilweise im Animationsfenster sichtbar ist. Zwar ist der Anwender mit den Scrollbars des Animationsfenster in der Lage, jeden Teil des Binärbaums anzuschauen. Beim Ablauf einer Animation ist der Anwender allerdings dabei überfordert, den Vorgang durch Bedienung der Scrollbars zu verfolgen, z.B. beim Einfügen wandert der neue Knoten zu einem Blatt. Droht nun die aktuelle Stelle der Animation aus dem Bild zu laufen, so wird dies durch das automatische Verschieben der vertikalen und/oder horizontalen Scrollbars verhindert. Somit ist gewährleistet, daß der Anwender jede Aktion mitverfolgen kann und dabei noch das Steuerunspanel bedienen kann.
Anhand der Problembeschreibung ergaben sich folgende potentielle Klassen, die im folgenden zum Teil näher mit ihren Attributen und Methoden beschrieben werden.
Klasse TreeNode
Beschreibung: Einzelner Knoten eines AVLTree.
Attribute
(1) Data: Schlüssel des Knoten Î {0..999}.
(2) BalanceFactor: Balancefaktor des Knoten Î {-2,-1,0,1,2}.
(3) Left, Right, Up: Zeiger auf anderen Knoten. Typ: TreeNode.
Objektverbindungen
(1) Verbindung zu AVLTree: Kardinalität :TreeNode 1 – AVLTree 0,m.
Klasse AVLTree
Beschreibung: Höhenbalancierter AVL-Baum.
Um die in dieser Klasse durchgeführten Baumoperationen später bei der Animation wieder genau rekonstruieren zu können, werden nach jeder Rotation die Daten des aktuellen Binärbaums (muss kein AVL-Baum sein) in einer verketteten Liste abgelegt. Zudem werden die Daten des Suchpfads in einer verketteten Liste festgehalten.
Attribute
(1) TreeTop: Wurzel des AVL-Baums. Typ: TreeNode.
(2) initPos: Aktuelle Baumdaten vor Rotation. Typ: VerkListe.
(3) leftRot: Baumdaten nach Linksrotation. Typ: VerkListe
(4) rightRot: Baumdaten nach Rechtsrotation. Typ: VerkListe
(5) suchPfad: Suchpfaddaten. Typ: VerkListe
Objektverbindungen
(1) Verbindung zu TreeNode: Kardinalität :AVLTree 0,m – TreeNode 1.
Methoden
(1) Delete(int x)
Wird x nicht im AVL-Baum gefunden, wird eine TreeDeleteMissing-Exception ausgeworfen. Andernfalls wird der Schlüssel gelöscht und notwendige Rotationen durchgeführt.
(2) Insert(x int)
Ist x bereits vorhanden, wird eine TreeInsertDuplicate-Exception ausgeworfen. Ansonsten wird x an einem Blatt angehängt und alle notwendige Rotationen ausgeführt.
(3) TreeToStack(TreeNode node, VerkListe vL, int x, int y, int hoehe)
Aktuelle Binärbaumdaten werden in einer verketteten Liste durch rekursive Traversierung (In-Order-Regel) abgelegt: Schlüssel, Balancefakor, x-Position, y-Position, Höhe linker Teilbaum und Höhe rechter Teilbaum.
(4) Rotate_Right_Child_Up (TreeNode CurrNode, TreeNode NextNode)
Durchführung der Linksrotation des Teilbaums von Wurzel CurrNode
(5) Rotate_Left_Child_Up(TreeNode CurrNode, TreeNode NextNode)
Durchführung der Rechtsrotation des Teilbaum von Wurzel CurrNode
Klasse StackNode
Beschreibung: Einzelnes Element einer verketteten Liste.
Attribute
(1) data: Schlüssel eines Knoten Î {0..999}.
(2) BalanceFactor: Balancefaktor eines Knoten Î {-2,-1,0,1,2}.
(3) x1: x-Postion auf Bildschirm des Knoten. Typ: Integer.
(4) y1: anlaog x1.
(5) left: Höhe linker Teilbaum des Knotens: Typ: Integer.
(6) right: analog left.
(7) Next: Zeiger auf nächstes Element. Typ: StackNode.
(8) Previous: Zeiger auf vorhergehendes Element. Typ: StackNode.
Objektverbindungen
(1) Verbindung zu VerkListe : Kardinalität :StackNode 1 – VerkListe 0,m.
Klasse VerkListe
Beschreibung: Beidseitig verkettete Liste.
Für die Verarbeitung der Daten bzgl. der Animation wurde die Datenstruktur einer verketteten Liste gewählt, da diese leicht zu handhaben ist und sequentiell abgearbeitet werden kann. Dabei repräsentiert jedes Element der verketteten Liste einen Knoten des AVL-Baums.
Attribute
(1) StackFirst: Erstes Element der verketteten Liste. Typ: StackNode.
(2) StackLast: Letztes Element der verketteten Liste. Typ: StackNode.
(3) StackCurrent: Aktuelles Element der verketteten Liste. Typ: StackNode.
Objektverbindungen
(1) Verbindung zu StackNode : Kardinalität :VerkListe 0,m – StackNode 1.
Methoden
(1) PushToEnd(int Data, int Balance, int x, int y, int left, int right)
Hängt der verk. Liste ein neues Element an.
(2) GoNext()
Geht vom aktuellen Element zum nächsten.
(3) GoPrev()
Aktuellen Zeiger zu vorhergehenden Element stellen.
(4) Length()
Gibt Länge der verketteten Liste zurück.
(5) Add(VerkListe x)
Hängt verkettete Liste an.
(6) delete(int Data)
Löscht entsprechendes Element aus der verketteten Liste.
Klasse ScrollableCanvas
Beschreibung: Legt ein Canvas und zwei Scrollbars an und legt diese in ein Panel ab. Benutzt ein BoderLayout, um die Scrollbars horizontal und vertikal anzulegen. Wenn die Scrollbars benutzt werden, verschiebt sich die Grafik. Durch eine Schnittstelle werden der Klasse die Grafiken in Form eines Images (Double-Puffering-Technik) zugeschickt und werden anschließend über dem Canvas ausgegeben.
Attribute
(1) offX: Aktuelle Position der horizontalen Scrollbar. Typ: Integer.
(2) offY: Aktuelle Position der vertikalen Scrollbar. Typ: Integer.
Methoden
(1) checkScrollbar(Scrollbar)
Überprüft, ob Scrollbar sich im definierten Wertebereich befindet.
(2) sentImage(Image)
Schnittstelle, um der Klasse ScrollableCanvas das Image, in der sich aufgebaute Grafiken befinden, zu senden. Unmittelbar danach wird paint()-Methode aufgerufen.
(3) paint(Graphics)
Gibt Inhalt der Image aus. Die offsetX und offsetY Variablen spezifizieren, welcher Teil von dem grösseren Image im relativ kleineren Canvas gezeigt werden soll.
(4) handelEvent()
Behandelt die Scrollbar-Events. Aktualisiert die offsetX und offsetY - Variablen. Nach jedem Events wird ein repaint() durchgeführt.
(5) reshape(int x, int y, int width, int heigt)
Diese Methode wird aufgerufen, wenn sich die Größe des Hauptfensters sich ändert. Dadurch können die Scrollbarwerte und Canvasdimension aktualisiert werden.
(6) setScrollbarValues(int x, int y)
Bewegt die Scrollbars automatisch, damit man alle Animationsaktionen sehen kann. Wenn bei einem Bewegungsvorgang Gefahr droht, daß die aktuelle Aktion aus dem sichtbaren Bereich läuft, werden die Scrollbarwerte angepaßt.
Klasse TreeDeleteMissing
Beschreibung: Exception wird ausgeworfen, wenn der zu löschende Schlüssel sich nicht im AVL-Baum befindet. Exception kann danach aufgefangen werden.
Klasse TreeInsertDuplicate
Beschreibung: Exception wird ausgeworfen, wenn der einzufügende Schlüssel sich bereits im AVL-Baum befindet. Exception kann danach aufgefangen werden.
Klasse DrawTree
Beschreibung: Zeichnet einen Binärbaum in ein Image anhand der übergebenen Baumdaten.
Attribute
Alle Grafiken werden zunächst in einem Puffer aufgebaut. Der wird (Double-Buffering). So wird verhindert, daß die Grafik sich gemächlich aufbaut. Typ: Image.
Methoden
(1) printNodeWithData1(Graphics g, VerkListe stack, Color color)
Knoten des Baumes mit Schlüssel werden anhand der Baumdaten von stack in Farbe color gezeichnet.
(2) printBalance(Graphics g, VerkListe stack, Color color)
Zeichnet in das obere Drittel des Konten den Balancefaktor in der Farbe color.
(3) printLines(Graphics g, VerkListe stack, Color color)
Zeichnet Linien, die die Knoten des Binärbaumes mit den Daten von stack verbinden. Dabei wird der Abstand zwischen den Knoten ermittelt und dann in der Farbe color die Verbindungen gezeichnet.
(4) printTree(Graphics g, VerkListe stack, Color NodeColor, Color BalColor)
Obige Methoden (1) bis (3) werden nacheinander aufgerufen und in offscreen gezeichnet.
Klasse DrawInsert
Beschreibung: Wird aufgerufen, wenn ein neues Element in den AVL-Baum eingefügt wird. Alle Bewegungen der Animation, die durch das Einfügen entstehen (blaue Linie nachziehen beim Einfügen, u.U. Rotation(en) mit blauem Pfeil, blaue Linie wieder neutraliseren, Textausgabe in Textarea) werden hier abgehandelt.
Attribute
(1) moveNode1: Daten der Bewegung der 1. Rotation. Typ: VerkListe.
(2) moveNode2: Daten der Bewegung der 2. Rotation. Typ: VerkListe
(3) moveInsert: Bewegungsdaten des einzufügenden Knotens. Typ: VerkListe.
(4) initTree: Baumdaten vor Rotation. Typ: VerkListe.
(5) rot1Tree: Baumdaten nach 1. Rotation. Typ: VerkListe.
(6) rot2Tree: Baumdaten anch 2. Rotation. Typ: VerkListe.
(7) einfPfad: Einfügepfaddaten. Typ: VerkListe.
(8) sleepTime: Pause des Threads zwischen den einzelnen Bewegungen. Typ: Integer.
Methode
(1) computeMoveInsert(VerkListe einfPfad)
Die Einfügebewegung wird berechnet. Zuerst wird eine Bewegung von oben senkrecht zur Wurzel eingefügt. Dann werden die Bewegungen von Knoten zu Knoten des Baumes entlang des Einfügepfads bis zum Endpunkt ermittelt und in moveInsert abgelegt.
(2) computeMoveNode(VerkListe stack1, VerkListe stack2)
Rotationsbewegung wird berechnet. In stack1 stehen alle Koordinaten der Knoten vor Rotation, in stack2 Koordinaten nach Rotation. Wenn sich die Koordinate eines Knoten sich verändert hat, wird die Bewegung mit Anfangskoordinate (stack1) nach Endkoordinate (stack2) ermittelt und in der Bewegungsliste abgelegt, die zurückgegeben wird.
(3) drawArrow()
Zeichnet einen blauen Pfeil in Rotationsrichtung überhalb der Rotation.
(4) printLinesBack(VerkListe stack, VerkListe baum, int b, int e)
Zeichnet von der aktuellen Stelle der Einfügebewegung bis zur Wurzel hin eine dicke blaue Linie.
(5) printThickLines (VerkListe stack, boolean direction)
Zeichnet eine dicke blaue Linie von der Wurzel bis zur aktuellen Stelle der Einfügebewegung entlang der Verbindungslienen des Baumes.
(6) nextCoordinate(VerkListe stack, int b, int e)
Berechnet Koordinaten der nächsten Bewegung. Die Bewegungsdaten stehen in stack. Im stack stehen die Anfangs- und Endkoordinaten jedes Knotens, der bewegt werden soll. Die Bewegungsdaten können entweder synchron oder sequentiell bearbeitet werden. Bei synchroner Bewegung werden alle Elemente gleichzeitig von ihrem Anfangspunkt bis zu ihrem Endpunkt bewegt, d.h. bei allen Elementen von stack wird der nächste Punkt berechnet. Bei sequentieller Abarbeitung wird zuerst das 1. Element zu seinem Endpunkt bewegt danach das 2.,3. usw., d.h. immer nur bei dem aktuellen Elememt wird die nächste Koordinate berechnet.
(7) moveReady(VerkListe stack)
Überprüft, ob alle Element in der Bewegungsliste stack ihren Endpunkt erreicht haben.
(8) run()
Kontrolliert den Einfügevorgang. Zuerst wird der neue Knoten an die richtige Stelle im Baum bewegt. Zugleich wird der Einfügepfad mit blauen Linie gekennzeichnet. Danach wird der Einfügepfad wieder zurückverfolgt. Bei jedem Knoten wird kontrolliert, ob eine Rotation notwendig ist.
Klasse DrawDelete
Beschreibung: Wird aufgerufen, wenn ein Element aus dem AVL-Baum gelöscht wird. Alle Bewegungen der Animation, die durch das Löschen entstehen (blaue Linie nachziehen beim Suchen des Elements, u.U. Rotation(en) mit blauem Pfeil, blaue Linie wieder neutraliseren, Textausgabe in Textarea) werden hier abgehandelt. Im Unterschied zum Einfügen können beim Löschen vorkommen mehrere Rotationen notwendig sein. Zudem existiert noch eine Mehtode, die das Vertauschen von Schlüsseln im Baum regelt.
Methoden
(1) arrangeMove(VerkListe stack1, VerkListe stack2)
Veranlaßt eine Rotation im Animationsfenster. Alle Baumdaten werden beim Löschen nur in einer verketteten Liste mit Trennzeichen abgelegt. Hier werden sie dann wieder voneinander getrennt. Alle notwendige Schritte für eine Rotation werden veranlaßt und schließlich durchgeführt.
(2) arrangeSwapMove(VerkListe stack1, VerkListe stack2, VerkListe stack3)
Führt eine Vertauschungsbewegung von zwei Knoten durch. Falls ein zu löschender Schlüssel im AVL-Baum ein innerer ist, muss dieser mit dem größten Schlüssel im linken Teilbaum vertauscht werden.
(3) run()
Kontrolliert den Löschvorgang. Alle Methoden werden von hier aufgerufen.
Klasse Demo
Beschreibung: Simuliert das Löschen und Einfügen von Schlüsseln. Einige werden durch Programmanweisungen zuerst eingefügt und dann wieder gelöscht. Dies dient dazu, dem Anwender die Animation vorzuführen, wobei interessante Fälle vorgeführt werden.
Klasse Hilfe
Beschreibung: Stellt das Hilfemenü der AVL-Baum-Animation dar. In einem separatem Fenster sind Erläuterungen zu alle Menüoptionen und Funtkionen abrufbar.
Klasse SpeedSelect
Beschreibung: Dient dazu, die Animationsgeschwindigkeit zu bestimmen. Dazu wird ein neues Fenster mit einer Scrollbar geöffnet, in der die Geschwindigkeit gerregelt werden kann.
Klasse Mainframe
Beschreibung: Baut das Hauptfenster mit Infofenster, Bedienungspanel, Animationsfenster und Steuerungspanel auf. Das zentrale Event-Handling wird von hier aus gesteuert, d.h. alle Klassenaufrufe (Ausnahme MainApplet) erfolgen aus dieser Klasse.
Attribute
(1) history: Alle durchgeführten Baumoperationen des aktuellen AVL-Baums werden in diesem Stack festgehalten, um eine Ungeschehen-Funktion zu ermöglichen. Typ: Stack.
(2) Tree: Aktueller AVL-Baum. Typ: AVLTree.
Methoden
(1) rekonstruiereBaum (Stack history, AVLTree avltree)
Baut einen neuen AVLTree anhand des Stacks history auf, d.h. alle getätigte Baumoperationen des aktuellen AVL-Baums können wieder sukzessive ungeschehen gemacht werden.
(2) addNewElement(int zahl, Thread thread)
Fügt im AVL-Baum ein neues Element zahl ein und ruft Klasse DrawInsert auf.
(3) deleteElement(int zahl, Thread thread)
Löscht im AVL-Baum Element zahl und ruft Klasse DrawDelete auf.
(4) handleEvent(Event event)
Fängt alle Ereignisse aus dem Hauptfentser auf und ruft enstprechende Methoden bzw. Klassen auf.
Klasse MainApplet
Beschreibung: Hauptklasse: Gibt den Text auf der Web-Seite aus und ruft die Klasse Mainframe auf.
Attribute
Wird an alle Klassen mit Threads mitübergeben, um Probleme mit suspend() und resume() zu verhindern. Grund: Klassen in Applets dürfen nur Threads manipulieren, die der selben ThreadGroup angehören, wie der public-Appletklasse.
Hinweis: Es ist auch mögliche eine fast vollständige Dokumentation zu AVLTree erhalten. Alle Kommentare zu Klassen, Konstruktoren, Methoden und Attributen wurden im Quelltext durch /**...*/ eingegrenzt. Dadurch ist es mit dem JDK mitgelieferten Hilfsprogramm javadoc möglich, HTML-Dateien im Format der API-Dokumentation zu erzeugen.
Um die Arbeitsweise von AVLTree besser nachvollziehen können, wird grob veranschaulicht, wie das Programm bei einem Einfügevorgang funktioniert.
Wenn der Anwender eine Zahl im Textfenster eingegeben hat und den Button ‘Schluessel einfuegen‘ drückt, wird folgender Mechanismus ausgelöst:
|
Klasse |
|
|
Mainframe |
Ereignis von Button ‘Schluessel einfuegen‘ wird aufgefangen. Aus dem Textfenster wird der Schlüssel eingelesen und die Methode addNewElement(int) aufgerufen. Dort wird versucht, einen neuen Schlüssel in den AVL-Baum einzufügen und die Buttons 'Schluessel einfuegen' und 'Schluessel loeschen' werden deaktiviert. |
|
TreeInsert-Duplicate |
Falls dieser Schlüssel sich bereits im Binärbaum befindet, wird eine TreeInsertDuplicate-Exception ausgeworfen und in addNewElement() aufgefangen. Daraufhin wird eine Meldung im Infofenster ausgegeben. |
|
AVLTree |
Anderfalls wird die Einfügestelle im AVL-Baum gesucht. |
|
TreeNode |
Es wird ein neuer Knoten angelegt und im AVL-Baum eingefügt. |
|
VerkListe |
Verkettete Listen, in denen alle Baumdaten abgelegt sind, werden angelegt. Dabei repräsentiert jede verkettete Liste einen Baum. |
|
StackNode |
Eine verkettete Liste besteht aus einer Anreihung von StackNodes. In diesen werden Informationen eines Knotens gespeichert. |
|
MainFrame |
Klasse MoveInsert wird aufgerufen. |
|
MoveInsert |
Mit den verketteten Listen werden Bewegungsabläufe berechnet und permanent in eine Offscreen gezeichnet und an das Animationsfenster (Klasse ScrollableCanvas) geschickt. |
|
ScrollableCanvas |
Erhält die ScrollableCanvas eine neue Offscreen, wird diese unmittelbar am Bildschirm ausgegeben. |
|
MainFrame |
Nach Beendigung der Animation werden die deaktivierten Buttons wieder freigegeben und weitere Operationen können durchgeführt werden. |
Abbildung 5.2 zeigt die Klassenhierarchie nach Coad/Yourdon-Notation. Klassen aus Java-Bibliotheken sind mit java.Bibliothekname.Klassenname bezeichnet. In der Darstellung wurde aus Gründen der der Komplexität darauf verzichtet, Attribute und Methoden der Klassen aufzuführen.
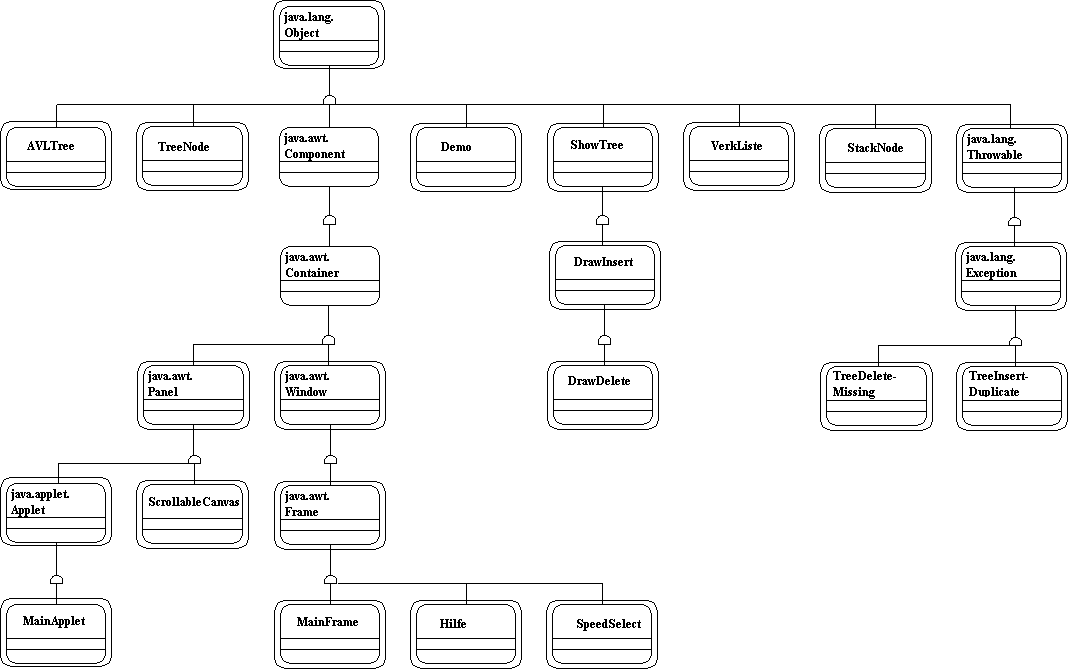
Abbildung 5.2: Klassenhierarchie des Programms AVLTree
Ausblick
Aufgrund des objektorientierten Entwurfs der Anwendung ist diese für Erweiterungen geeignet. So wäre es möglich, das Applet um weitere Animationen zu erweitern. Beispielsweise wäre es möglich noch eine Demonstration zum gewichtsbalancierten BB(a )-Baum hinzuzufügen werden. Es müssten dann vier weitere Klassen entwickelt werden. Eine Klasse wäre für den BB(a )-Baum erforderlich und eine weitere für dessen Knoten. Für die Animation müssten noch die Klassen für das Einfügen und Löschen entwickelt werden.
Da zu Beginn der Studienarbeit kein besonderes Augenmerkmal auf die Erweiterbarkeit gelegt wurde, sind die Klassen MoveInsert und MoveDelete leider nur für AVL-Bäume geeignet. Da das Herz der Animation diese beiden Klassen darstellen, hätte unter dem Aspekt der Weitervewendung und Übersichtlichkeit eine feinere Einteilung in weitere Klassen erfolgen können. So wäre eine reine Bewegungsklasse, die Objekte von einer Start- zu einer Endposition bewegt, sinnvoll gewesen. Diese hätte dann auch für Erweiterungen genutzt werden können. Wie bei der Klasse TreeNode, die einen Knoten im AVL-Baum darstellt, hätte eine Klasse eingeführt werden können, die einen Knoten graphisch definiert. Die Klasse ShowTree hätte dann die Aufgabe gehabt, einen grafisch definierte Knoten einzubinden und mit diesem einen Binärbaum optisch aufzubauen. Weiterhin wäre bei einer Erweiterung möglich gewesen, jede spezielle Baumart auf eine spezielle Weise darzustellen. Beim BB(a )-Baum beispielsweise wird anstatt eines Balancefaktors ein sogenanntes Gewicht mitgeführt, welches eine reelle Zahl ist und zwischen 0 und 1 liegt.
Der folgende Verbesserungsvorschlag, der nicht mehr realisiert wurde, wäre dann auch leichter umsetzbar gewesen. Die Möglichkeit, die Größe der Knoten bzw. der Schrift individuell zu gestalten oder zumindest drei auswählbare Größen anzubieten, hätte die Unabhängigkeit von der Bildschirmgröße und dessen Auflösung deutlich gefördert. So wäre jeder Benutzer in der Lage gewesen, das richtige Maß zwischen Gesamtübersicht und Leserlichkeit selbst zu regulieren und auf seine Hardware abzustimmen.
Das Ziel des Tele-Teaching ist es unter anderem den Vorlesungsstoff multimedial aufzubereiten. Bei dieser Studienarbeit fehlt bisher allerdings noch die Audio-Unterstützung. Denkbar wäre das Hinzufügen von kurzen Sequenzen gewesen, die abgespielt werden, wenn wichtige Ereignisse eintreten. Der Anwender wäre so auf wichtige Aktionen noch mehr sensibilisiert worden. Das Infofenster, welche dokumentiert, was momentan im Aktionfenster geschieht, ist wichtig, damit der Anwender auch die theoretische Hintergründe erfährt. Es enststeht dabei folgendes Problem. Der Benutzer wird überfordert, gleichzeitig das Info- und Animationsfenster im Auge zu behalten. Zwar besteht die Möglichkeit, den Animationsablauf mit dem Steuerungspanel zu unterbrechen, um im Infofenster alles nachlesen zu können. Durch das Hin- und Herschalten geht aber der flüssige Ablauf verloren und könnte den Anwender mit der Zeit stören. An dieser Stelle wäre die Audio-Unterstützung von großer Hilfe gewesen. Zusätzlich zum Infofenster hätten die Information auch über Lautsprecher ausgegeben weden können. Außerdem werden erfahrungsgemäß sehr gute Lerneffekte durch gleichzeitges Sehen und Hören erzielt.
Das Einbinden von Audio-Effekten stellt keine großer Herausforderung dar, ist aber mit viel Arbeit verbunden. Es bestehen Überlegungen, dies noch für dieses Programm nachzuholen.
Der Anwender ist jederzeit in der Lage, aktiv in die Animation einzugreifen und kann dabei individuell sein Lernen gestalten. Dabei werden alle Informationen und letztendlich auch alle Lösungen im Infofenster angegeben. Dabei besteht die Gefahr, daß der Anwender zwar die Animation aktiv steuert, aber ihr lerntechnisch zu wenig Aufmerksamkeit spendet. Es könnte sogar seitens des Anwenders eine Passivität entstehen. Diese Phänomen ist auch in Vorlesungen zu beobachten, in denen Studenten nicht mit Gegenfragen rechnen müssen und eine passive Stellung einnehmen. Um dem entgegenzuwirken und den Benutzer noch mehr in das Programm einzubeziehen, wäre eine Option denkbar gewesen, die zuläßt einen Lernmodus einzuschalten. Dies könnte folgendermaßen aussehen: der Anwender wird immer vor entscheidenden Stellen im Animationsablauf in einer Dialogbox nach seinem bisherigen Wissen abgefragt wird. So müßte der Anwender dann beispielsweise entscheiden, ob eine Rotation bevorsteht und diese auch benennen. Vorstellbäre wäre auch eine Steigerung des Schwierigkeitsgrades, bei dem der Anwender immer frühzeitiger erkennen muß, welche Rotation notwendig ist. Das Ganze könnte man dann wiederum mit Audio-Unterstützung gestalten und z.B. den Anwender bei Erfolgen loben.
Nach Startschwierigkeiten steigern sich oftmals nach ersten Ergebnissen und Erfolgen oft die Motivation und der Drang nach Perfektionismus. Dies war bei dieser Studienarbeit nicht anderst. Allerdings hätte die Umsetzung aller aufgezählten Verbesserungsvorschläge den Rahmen dieser Studienarbeit gesprengt. So konnten nur auf die wichtigsten Aspekte eingegangen werden.
Sollte die multimediale Unterstützung der Vorlesung auf ein positives Echo stoßen ist nicht ausgeschlossen, daß der eine oder andere Verbesserungsvorschlag zukünftig doch noch verwirklicht wird.
[JM96] Jackson Jerry R. / McClellan Alan L.: JAVA by Example, 1st edition, Sun Microsystems, Inc., 2550 Garcia Avenue, Mountain View, California, 1996.
[F96] Flanagan David: Java in a Nutshell, 1st edition, O'Reilly & Associates, Inc., 103 Morris Street, Siute A, CA 95472, 1996.
[CH96] Cornell Gary / Hoffmann Cay S.: Java bis ins Detail, 1. Auflage, Heise Verlag , Hannover, 1996
[CY92] Coad Peter / Yourdon Edward: Object-Oriented Analysis, 2nd edition, Yourdon Press, Prentice Hall, Englewood Cliffs, 1992.
[KS96] Kuhlins Stefan / Schader Martin: Objekorientierte Systemanalyse, 2. Auflage,Springer-Verlag Berlin u.a., 1996.
[OW96] Ottmann T. / Widmayer P.: Algorithmen und Datenstrukturen, 3. Auflage, Spektrum Akademischer Verlag, Heidelberg, Berlin, Oxford, 1996.
[W86] Würth Niklaus: Algorithmen und Datenstrukturen, 4. Auflage, B. G. Teubner Stuttgart, 1986.
[EEG97] Effelsberg W., Eckert A., Geyer W.: A Distance Learning System for Higher Education Based on Telecommunication and Multimedia, Mannheim, 1997